第46回「3D図形の作図関数」

今回はスクリプトでの3D作図の基本のおさらいです。VectorScript・Pythonを使用して3D図形を描くプログラムを紹介します。（執筆：A&A川崎）

3D図形のプログラミングを通して、VectorScript・Pythonのプログラムの基本的な書き方に慣れていきましょう。Vectorworksのプログラミングでは、3D図形のAPIが目的ごとに用意されているので、短いコードで簡単に3Dの図形を作図することができます。

3D作図のAPIは目的がはっきりしたシンプルな関数群となっていますが、実際に関数を使うとき、関数の組み合わせや引数のルールのところで「どうやって使うんだっけ」となりやすい部分です。今回、実際に3Dの図形を描くことでプログラムで何をやっているのか直感的に理解して、体に染み込ませておきましょう。

今回は基本編の内容となりますので、Vectorworksプログラミングにご興味をお持ちの方、この機会にぜひチャレンジしてください。プログラムを使用して図形を描く場合でも結果としてはVecctorworks標準のツールにある図形と同じものが描かれますので、手動で描く場合と比較しながら（プログラムを）描いてみてください。

46-1. 3D基準点

手動で描く場合、3D基準点ツールを選択し、描きたいところでマウスをクリックします。

プログラムで描く場合、手続きLocus3Dを使います。

VectorScript:

PROCEDURE Locus3D( pX : REAL; pY : REAL; pZ : REAL );

Python:

def vs.Locus3D( p ) : return None

3D基準点を描きたい位置の3D座標x,y,zを引数に指定します。Pythonはタプル型で指定します。ここでは3D基準点を4点作図するプログラムを作成します。

VectorScript:

PROCEDURE kijyunten3D; 
BEGIN
    Locus3D( -50.0, -50.0, 0.0 );
    Locus3D( 50.0, -50.0, 0.0 );
    Locus3D( 50.0, 50.0, 0.0 );
    Locus3D( 50.0, 50.0, 200.0 );
END;
Run( kijyunten3D );

Python:

vs.Locus3D( ( -50.0, -50.0, 0.0 ) );
vs.Locus3D( ( 50.0, -50.0, 0.0 ) );
vs.Locus3D( ( 50.0, 50.0, 0.0 ) );
vs.Locus3D( ( 50.0, 50.0, 200.0 ) );

実行すると、3D基準点が指定した座標に4点作図されました。

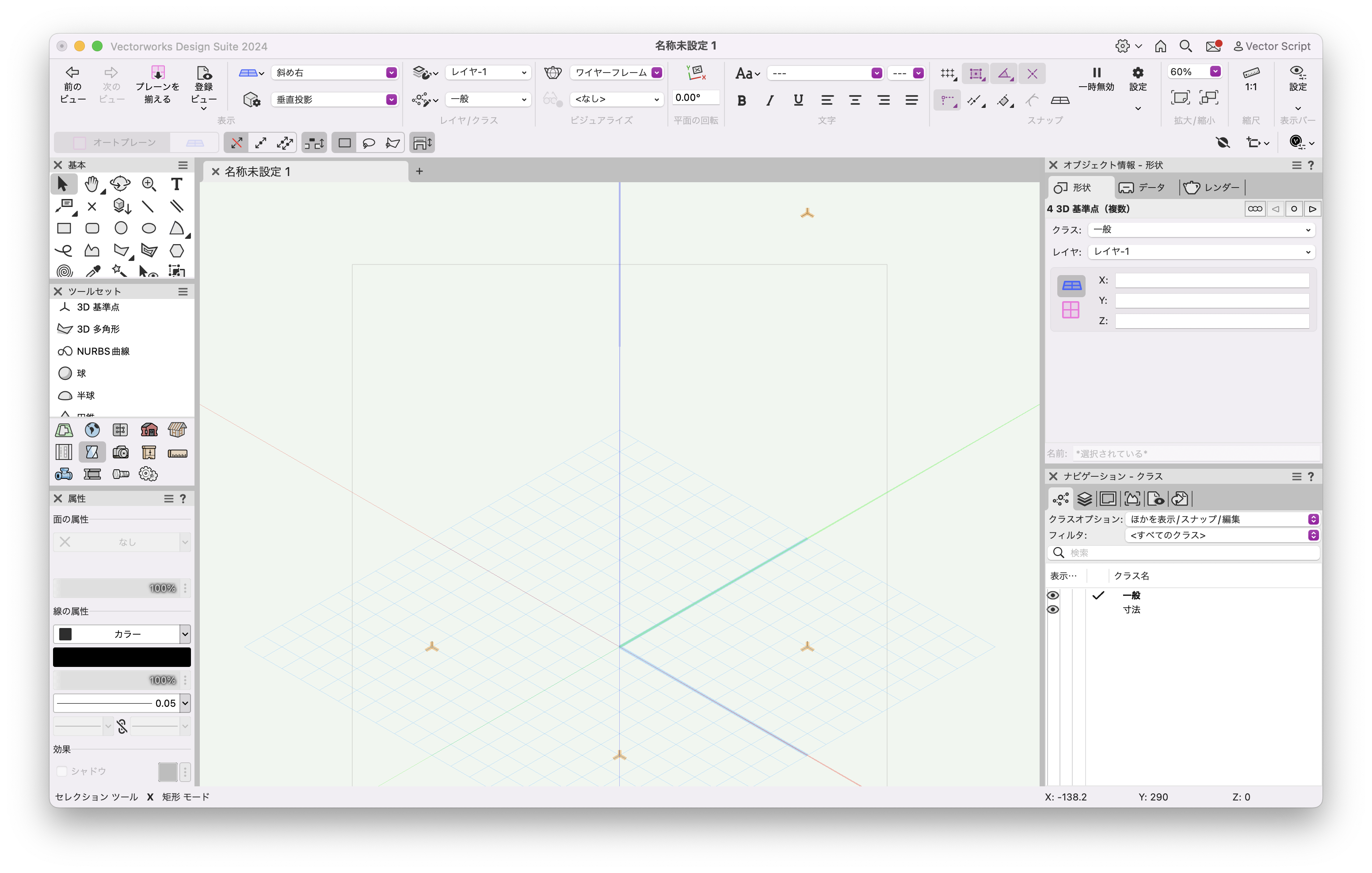
※ 3D基準点はワイヤーフレームでのみ表示される場合があります。環境設定>画面>3D基準点の表示の設定を確認してください。

46-2. 3D多角形

手動で描く場合、3D多角形ツールを選択し、描きたいところで頂点の数だけマウスをクリックします。

プログラムでは、手続きBeginPoly3D、手続きEndPoly3D、手続きAdd3DPtを組み合わせて使います。

VectorScript:

PROCEDURE BeginPoly3D;
PROCEDURE EndPoly3D;
PROCEDURE Add3DPt( pX : REAL; pY : REAL; pZ : REAL );

Python:

def vs.BeginPoly3D() : return None
def vs.EndPoly3D() : return None
def vs.Add3DPt( p ) : return None

BeginPoly3Dで3D多角形の作図の開始を宣言して、EndPoly3Dで3D多角形の作図を終了します。その間でAdd3DPtを使用して3D多角形の頂点を一つずつ追加します。Add3DPtには3D多角形の頂点とする3D座標(x,y,z)を指定します。

ここでは4つの頂点をもつ3D多角形を作図するプログラムを作成します。

VectorScript:

PROCEDURE zukeiPoly3D;
BEGIN
    BeginPoly3D;
        Add3DPt( -50.0, -50.0, 0.0 );
        Add3DPt( 50.0, -50.0, 0.0 );
        Add3DPt( 50.0, 50.0, 0.0 );
        Add3DPt( 50.0, 50.0, 200.0 );
    EndPoly3D;
END;
Run( zukeiPoly3D );

Python:

vs.BeginPoly3D()
vs.Add3DPt( ( -50.0, -50.0, 0.0 ) )
vs.Add3DPt( ( 50.0, -50.0, 0.0 ) )
vs.Add3DPt( ( 50.0, 50.0, 0.0 ) )
vs.Add3DPt( ( 50.0, 50.0, 200.0 ) )
vs.EndPoly3D()

Pythonではvs.BeginPoly3D()やvs.EndPoly3D()のように、引数がない場合でも関数の後に()が必要になります。忘れてしまうと正常に動作しませんので注意しましょう。実行すると、4つの頂点をもつ3D多角形が作図されました。

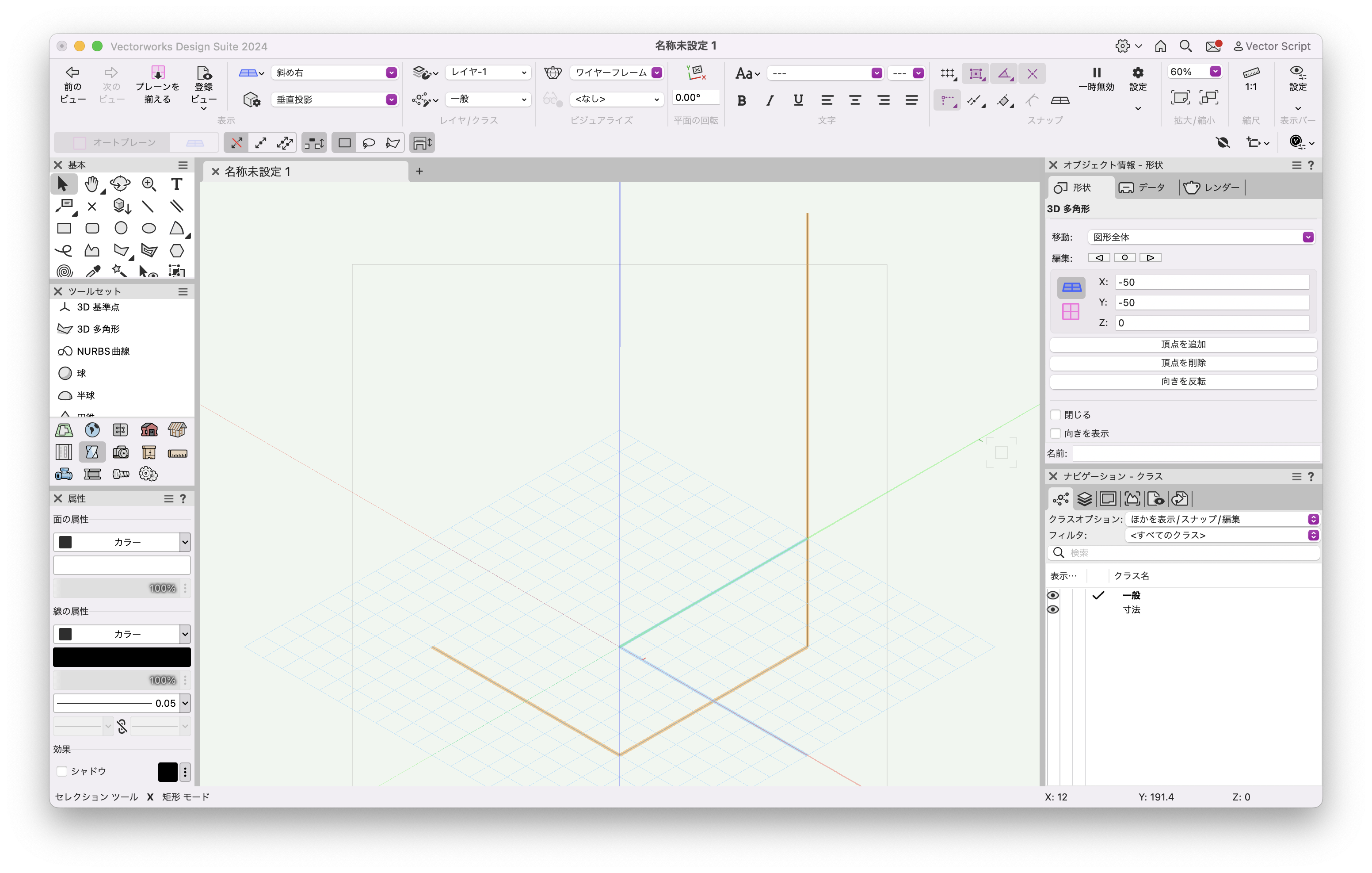
上記の方法の他にも、3D多角形を作図することができる手続があります。

VectorScript:

PROCEDURE Poly3D( p : REAL; );

Python:

def vs.Poly3D( p ) : return None

Poly3Dは、引数に頂点の数だけx,y,z座標を指定します。可変長の引数となっておりVectorworksのスクリプトでは珍しい種類です。BeginPoly3DやEndPoly3Dが不要なため、短いコードで書くことができます。一方で、頂点座標を引数に羅列する必要があり、コードの可読性の面で劣ります。

ここでは先ほどと同じ3D座標を指定します。

VectorScript:

PROCEDURE zukeiPoly3D;
BEGIN
    Poly3D( -50.0, -50.0, 0.0, 50.0, -50.0, 0.0, 50.0, 50.0, 0.0, 50.0, 50.0, 200.0 );
END;
Run( zukeiPoly3D );

Python:

import vs

vs.Poly3D( ( -50.0, -50.0, 0.0 ), ( 50.0, -50.0, 0.0 ), ( 50.0, 50.0, 0.0 ), ( 50.0, 50.0, 200.0 ) );

実行すると、上で作成したものと同じ形状の3D多角形が作図されます。

46-3. 柱状体

手動で描く場合、底面になる2D図形を選択した状態で、モデルメニューから「柱状体…」を実行します。

プログラムでは、手続きBeginXtrd、手続きEndXtrdと、任意の2D図形の作図APIを組み合わせて使います。

VectorScript:

PROCEDURE BeginXtrd( startDistance : REAL (Coordinate); endDistance : REAL (Coordinate) );
PROCEDURE EndXtrd;

Python:

def vs.BeginXtrd( startDistance, endDistance ) : return None
def vs.EndXtrd() : return None

3D多角形と同様に、BeginXtrdで柱状体の作図の開始を宣言して、EndXtrdで柱状体の作図を終了します。その間で柱状体の底面となる2D図形を作図します。BeginXtrdには柱状体の下端と上端の高さを引数に指定します。

ここでは100×100の四角形を底面に持ち、下端100、上端300の柱状体を作図するプログラムを作成します。

VectorScript:

PROCEDURE zukeiXtrd;
BEGIN
    BeginXtrd( 100.0, 300.0 );
    Rect( -50.0, 50.0, 50.0, -50.0 );
    EndXtrd;
END;
Run( zukeiXtrd );

Python:

vs.BeginXtrd( 100.0, 300.0 )
vs.Rect( ( -50.0, 50.0 ), ( 50.0, -50.0 ) )
vs.EndXtrd()

実行すると100〜300の高さの柱状体が作図されます。

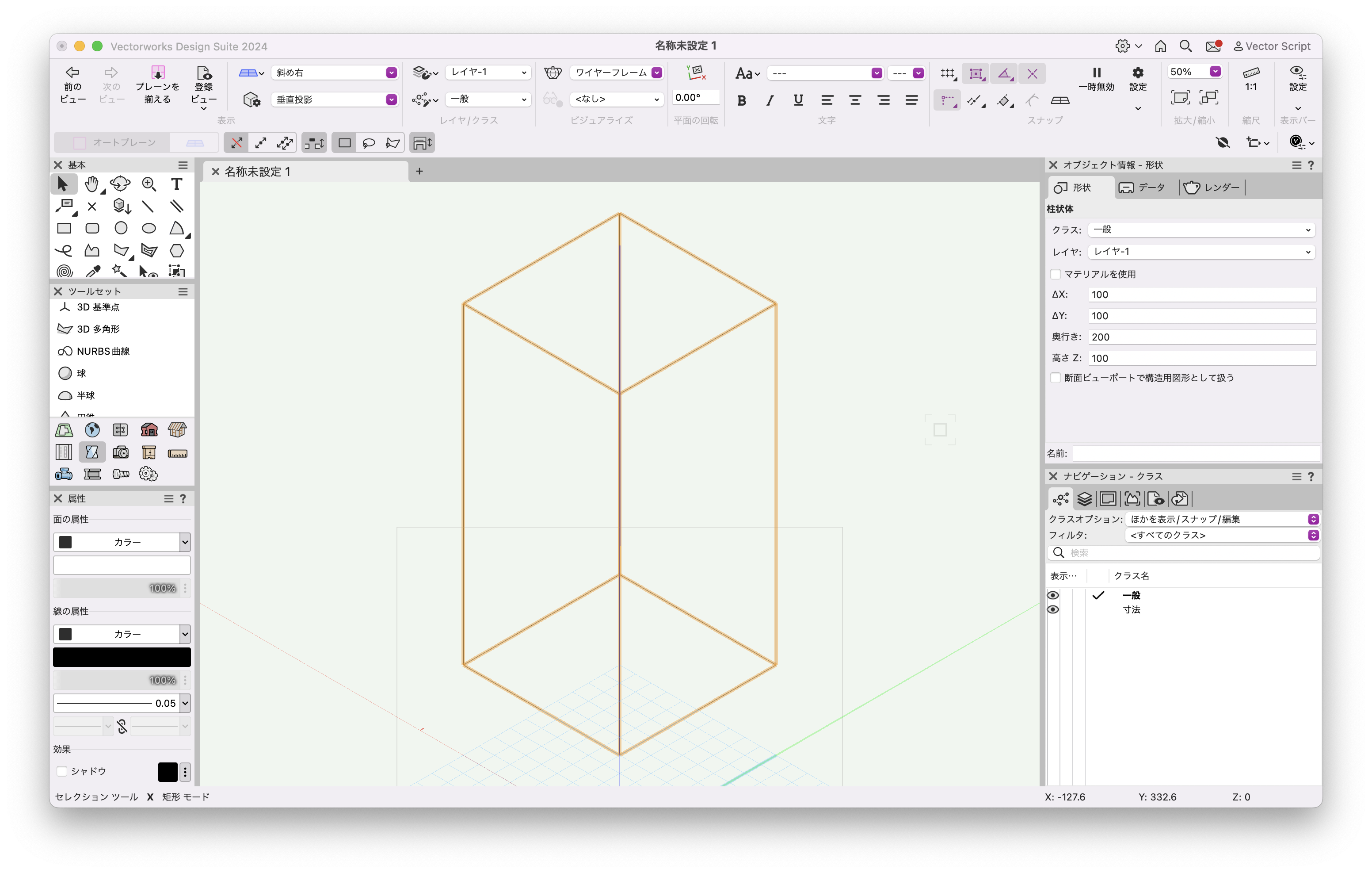
46-4. 多段柱状体

手動で描く場合、底面、中間面、上面になる2D図形を選択した状態で、モデルメニューから「柱状体…」を実行します。

プログラムで描く場合、手続きBeginMXtrd、手続きEndMXtrdと、各面の2D図形を作図するAPIを組み合わせて使います。

VectorScript:

PROCEDURE BeginMXtrd( startDistance : REAL (Coordinate); endDistance : REAL (Coordinate) );
PROCEDURE EndMXtrd;

Python:

def vs.BeginMXtrd( startDistance, endDistance ) : return None
def vs.EndXtrd() : return None

3D多角形や柱状体と同様に、多段柱状体ではBeginMXtrdとEndMXtrdの間で底面、中間面、上面になる3D図形を描きます。BeginMXtrdには多段柱状体の下端と上端の高さを引数に指定します。

ここでは5つの四角形の多段面を持つ、下端100、上端300の多段柱状体を作図するプログラムを作成します。

VectorScript:

PROCEDURE zukeiMXtrd;
BEGIN
    BeginMXtrd( 100.0, 300.0 );
        Rect( -100.0, 100.0, 100.0, -100.0 );{下面}
        Rect( -75.0, 75.0, 75.0, -75.0 );{中間面}
        Rect( -100.0, 100.0, 100.0, -100.0 );{中間面}
        Rect( -75.0, 75.0, 75.0, -75.0 );{中間面}
        Rect( -100.0, 100.0, 100.0, -100.0 );{上面}
    EndMXtrd;
END;
Run( zukeiMXtrd );

Python:

vs.BeginMXtrd( 100.0, 200.0 )
vs.Rect( ( -100.0, 100.0 ), ( 100.0, -100.0 ) )
vs.Rect( ( -75.0, 75.0 ), ( 75.0, -75.0 ) )
vs.Rect( ( -100.0, 100.0 ), ( 100.0, -100.0 ) )
vs.Rect( ( -75.0, 75.0 ), ( 75.0, -75.0 ) )
vs.Rect( ( -100.0, 100.0 ), ( 100.0, -100.0 ) )
vs.EndMXtrd()

プログラムを実行すると指定した5つの多段面をもつ多段柱状体が作図されます。

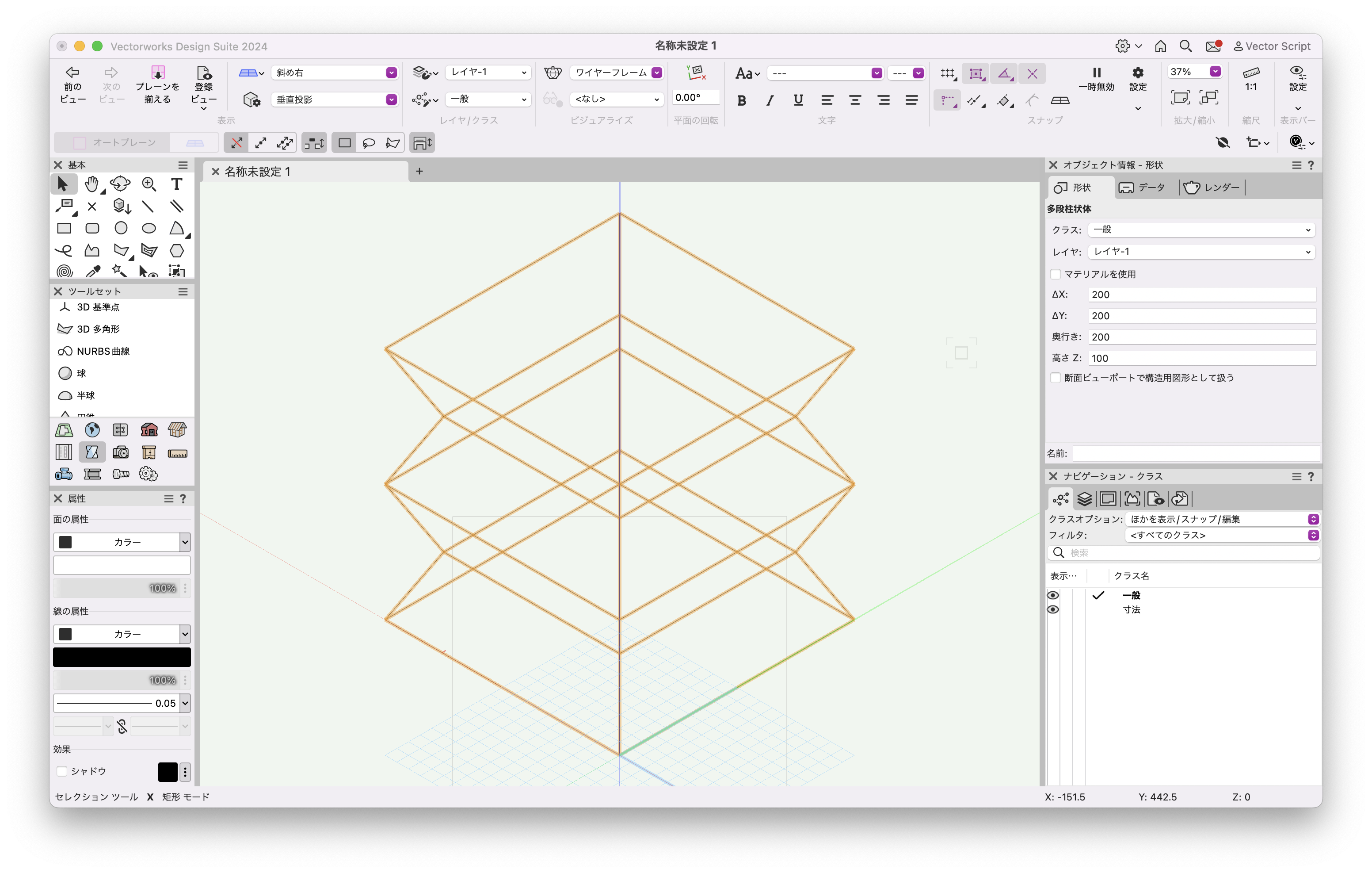
46-5. 3Dパス図形

手動で描く場合、断面になる2D図形と、3D多角形を選択した状態で、モデルメニューの「3Dパス図形…」を実行します。

プログラムでは、関数CreateExtrudeAlongPathを使います。

VectorScript:

FUNCTION CreateExtrudeAlongPath( pathHandle : HANDLE; profileHandle : HANDLE ) : HANDLE;

Python:

def vs.CreateExtrudeAlongPath( pathHandle, profileHandle ) : return HANDLE

事前に、断面の2D図形と、パス図形を用意する必要があります。手で描いたものでもいいですし、プログラムで作図したものでもいいです。

ここでは、パスの3D多角形と断面となる円をプログラム内で作図して、関数CreateExtrudeAlongPathの引数として渡します。

VectorScript:

PROCEDURE zukeiExtrudeAlongPath;
VAR
    pathHandle : HANDLE;
    profileHandle : HANDLE;
    objH : HANDLE;
BEGIN
    Poly3D( -50.0, -50.0, 0.0, 50.0, -50.0, 0.0, 50.0, 50.0, 0.0, 50.0, 50.0, 200.0 );
    pathHandle := LNewObj;
    ArcByCenter( 0.0, 0.0, 10.0, 0.0, 360.0 );
    profileHandle := LNewObj;
    objH := CreateExtrudeAlongPath( pathHandle, profileHandle );
END;
Run( zukeiExtrudeAlongPath );

Python:

vs.Poly3D( ( -50.0, -50.0, 0.0 ), ( 50.0, -50.0, 0.0 ), ( 50.0, 50.0, 0.0 ), ( 50.0, 50.0, 200.0 ) )
pathHandle = vs.LNewObj()
vs.ArcByCenter( 0.0, 0.0, 10.0, 0.0, 360.0 )
profileHandle = vs.LNewObj()
objH = vs.CreateExtrudeAlongPath( pathHandle, profileHandle )

プログラムを実行すると、円を断面とする3Dパス図形が作図されました。

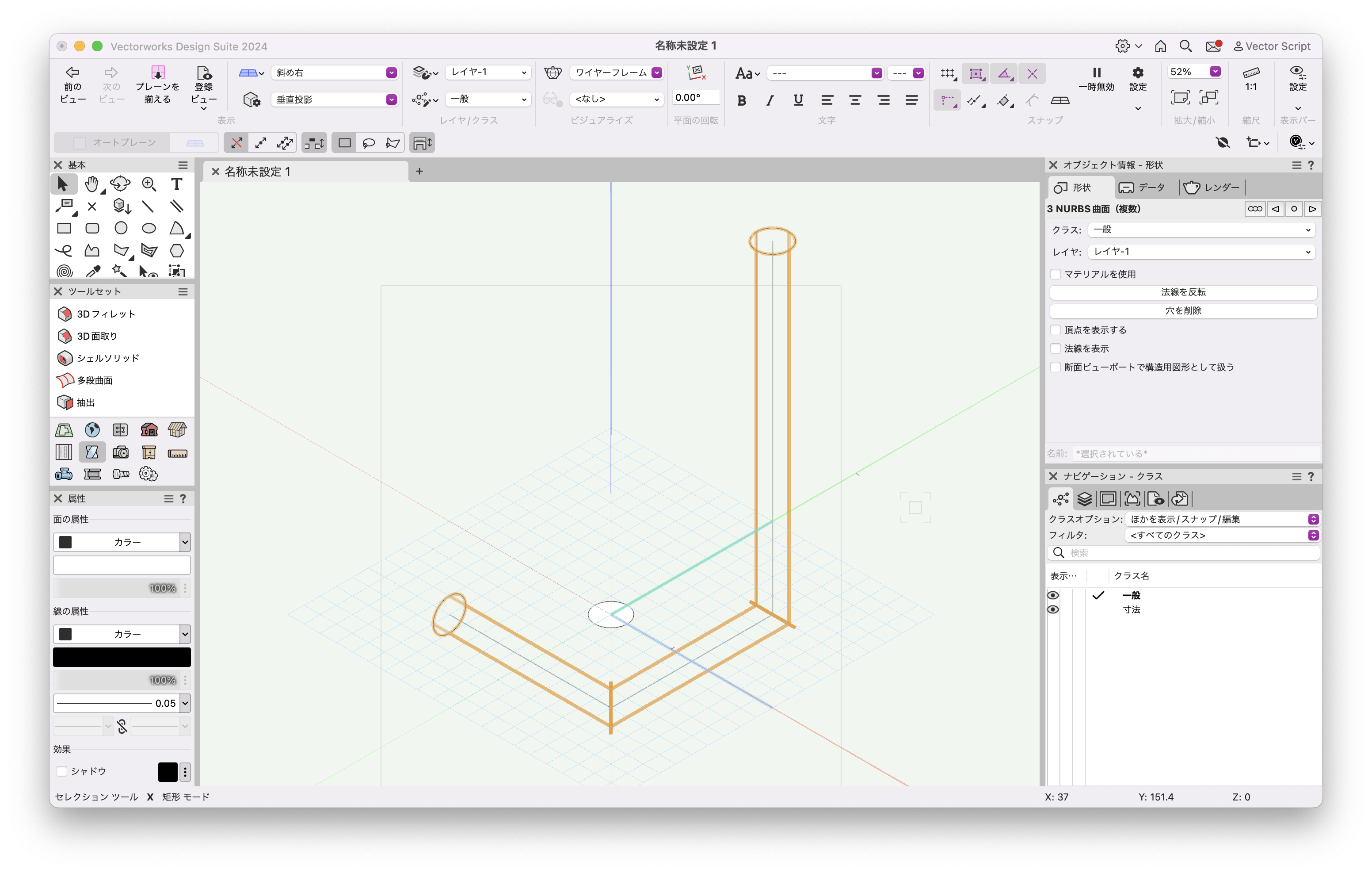
46-6. 錐状体（汎用ソリッド）

手動で描く場合、断面になる2D図形と、3D多角形を選択した状態で、モデルメニューの「錐状体…」を実行します。

プログラムで描く場合、関数CreateTaperedExtrd2と、底面の2D図形作図するAPIを組み合わせて使います。

VectorScript:

FUNCTION CreateTaperedExtrd2( profileH : HANDLE; angle : REAL; height : REAL ) : HANDLE;

Python:

def vs.CreateTaperedExtrd2( profileH, angle, height ) : return HANDLE

底面になる2D図形のハンドルを関数CreateTaperedExtrd2の引数として渡します。

ここでは半径10の円を底面として、角度5、高さ100の錐状体をを作成します。

VectorScript:

PROCEDURE zukeiTaperedExtrud2;
VAR
    objH : HANDLE;
BEGIN
    ArcByCenter( 0.0, 0.0, 10.0, 0.0, 360.0 );
    objH := CreateTaperedExtrd2( LNewObj, 5.0, 100.0 );
END;
Run( zukeiTaperedExtrud2 );

Python:

vs.ArcByCenter( 0.0, 0.0, 10.0, 0.0, 360.0 )
vs.CreateTaperedExtrd2( vs.LNewObj(), 5.0, 100.0 )

実行すると、円を底面とする錐状体が作成されました。

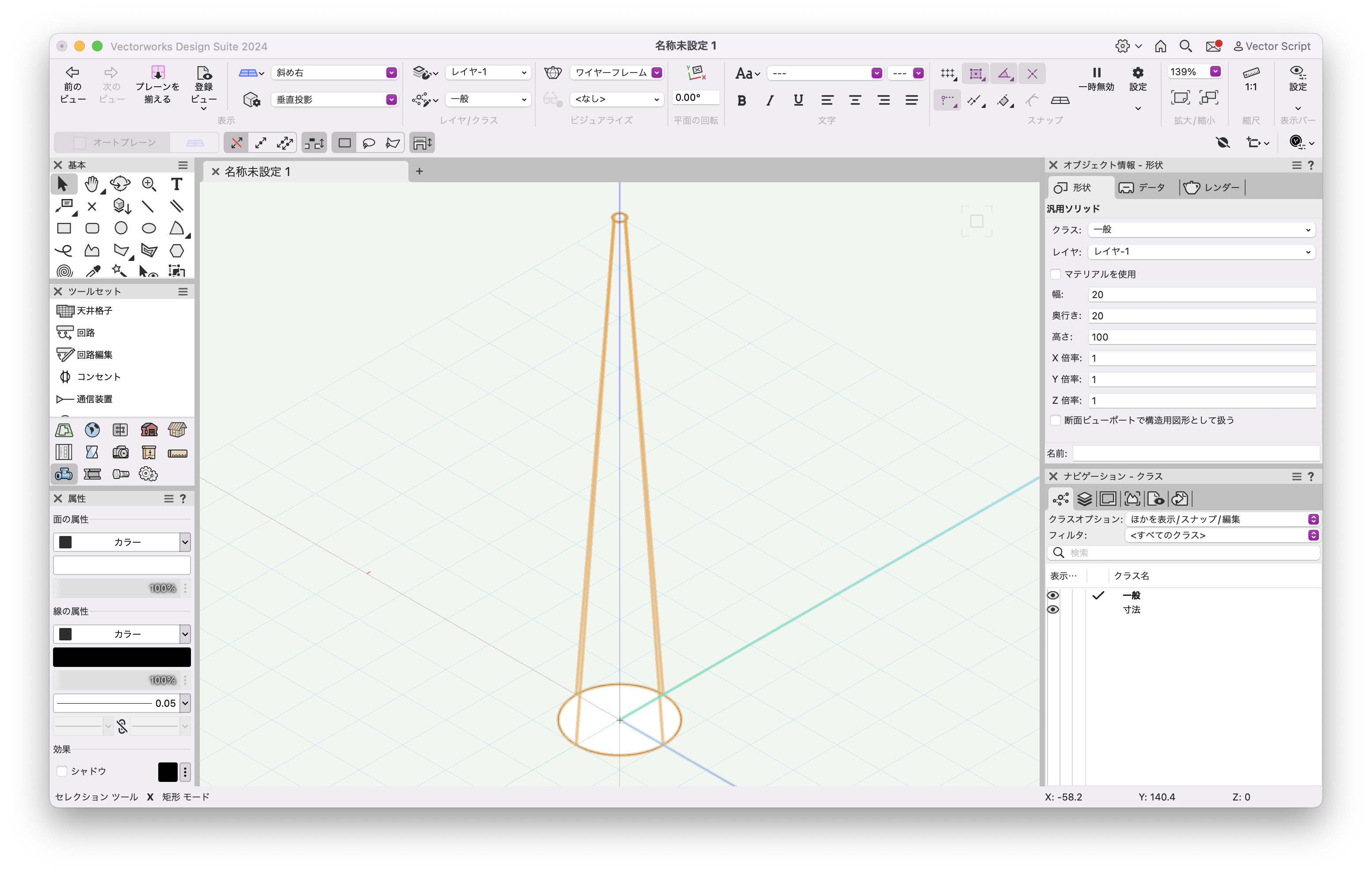
46-7. 回転体

手動で描く場合、断面になる2D図形を選択した状態で、モデルメニューから「回転体…」を実行します。

プログラムで描く場合、手続きBeginSweep、手続きEndSweepと、底面とする2D図形を作図するAPIを組み合わせてを使います。

VectorScript:

PROCEDURE BeginSweep( startAngle : REAL; arcAngle : REAL; incAngle : REAL; PitchDistance : REAL (Coordinate) );
PROCEDURE EndSweep;

Python:

def vs.BeginSweep( startAngle, arcAngle, incAngle, PitchDistance ) : return None
def vs.EndSweep() : return None

柱状体などと同様に、BeginSweepとEndSweepの間で底面になる2D図形を描きます。

BeginSweepには、開始角度、回転角度、回転の分割数、回転のズレを引数に指定します。

VectorScript:

PROCEDURE zukeiSweep;
BEGIN
    BeginSweep( 0.0, 360.0, 1, 100.0 );
        Rect( -50.0, 50.0, 50.0, -50.0 );
    EndSweep;
END;
Run( zukeiSweep );

Python:

vs.BeginSweep( 0.0, 360.0, 1, 100.0 )
vs.Rect( -50.0, 50.0, 50.0, -50.0 )
vs.EndSweep()

プログラムを実行すると、回転体が作図されました。

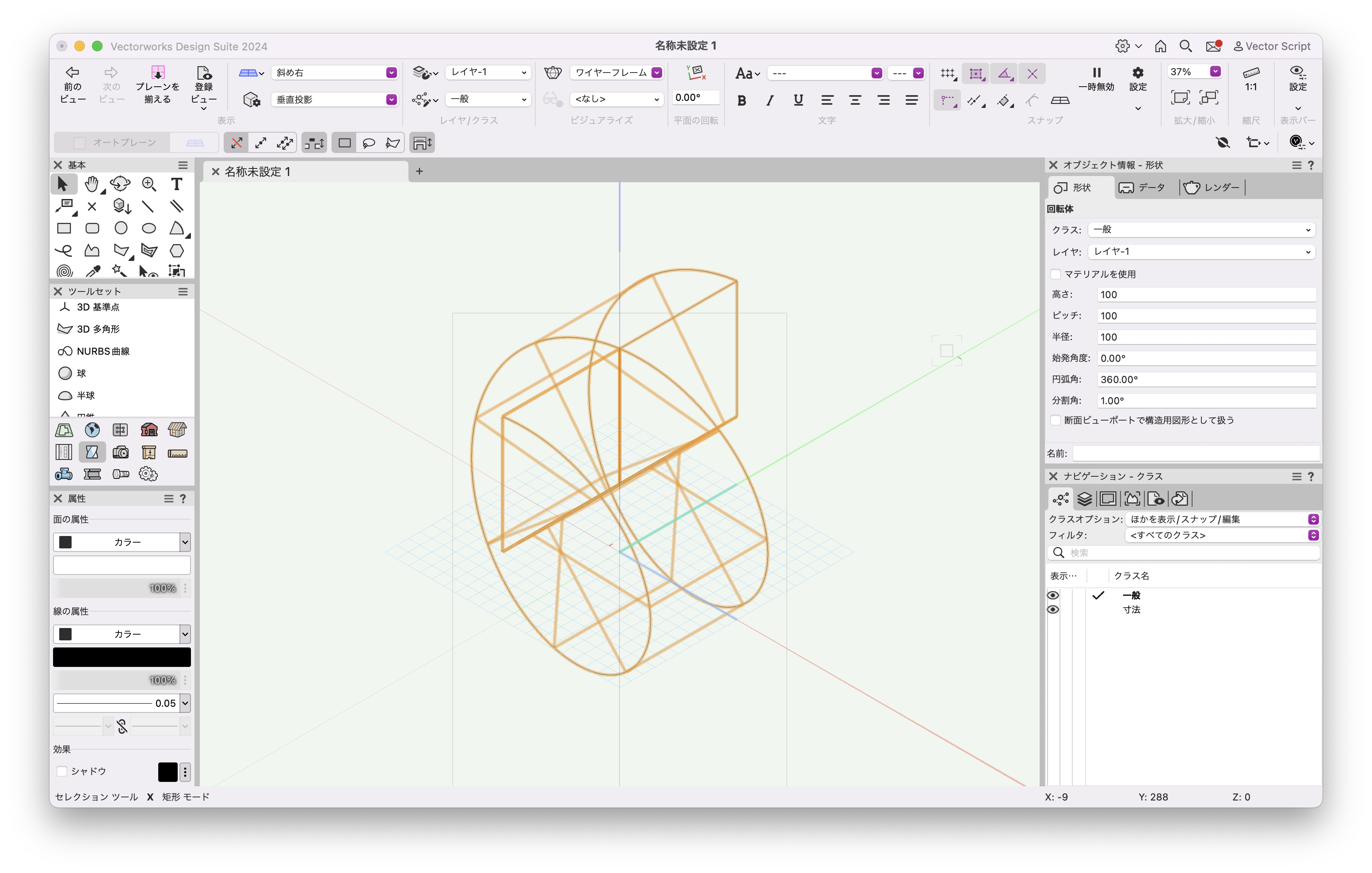
この機能を利用できる製品

	Vectorworks Fundamentals 2D/3D汎用作図機能に、プレゼンボード作成機能や図面と連動できる表計算機能など、数多くの基本作図機能に加え、高品質レンダリング&3Dビジュアライズ機能を搭載したVectorworksシリーズの基本製品詳細情報　購入ページ
	Vectorworks Architect 建築設計や内装、ディスプレイデザインに対応した先進的なBIM・インテリア設計支援機能、拡張機能、さらには豊富な建築向けのデータライブラリを搭載した建築/内装業界向け製品詳細情報　購入ページ
	Vectorworks Landmark 地形モデルや多彩な植栽、灌水設備計画等に対応するランドスケープデザイン機能、さらには豊富な造園向けのデータライブラリを搭載した都市計画/造園業界向け製品詳細情報　購入ページ
	Vectorworks Spotlight ステージプランニングやライティング計画に対応した先進的な舞台照明計画支援機能、さらには各種メーカー製のトラスや照明機材、音響機器等の豊富なデータライブラリを搭載したエンタテインメント業界向け製品詳細情報　購入ページ
	Vectorworks Design Suite 専門分野別（建築設計/ディスプレイデザイン、ランドスケープデザイン、ステージデザイン&スポットライトプランニング）の設計支援機能、拡張機能、さらには豊富なデータライブラリを搭載した最上位の製品詳細情報　購入ページ

	Vectorworks Fundamentals 2D/3D汎用作図機能に、プレゼンボード作成機能や図面と連動できる表計算機能など、数多くの基本作図機能に加え、高品質レンダリング&3Dビジュアライズ機能を搭載したVectorworksシリーズの基本製品詳細情報　購入ページ
	Vectorworks Architect 建築設計や内装、ディスプレイデザインに対応した先進的なBIM・インテリア設計支援機能、拡張機能、さらには豊富な建築向けのデータライブラリを搭載した建築/内装業界向け製品詳細情報　購入ページ
	Vectorworks Landmark 地形モデルや多彩な植栽、灌水設備計画等に対応するランドスケープデザイン機能、さらには豊富な造園向けのデータライブラリを搭載した都市計画/造園業界向け製品詳細情報　購入ページ
	Vectorworks Spotlight ステージプランニングやライティング計画に対応した先進的な舞台照明計画支援機能、さらには各種メーカー製のトラスや照明機材、音響機器等の豊富なデータライブラリを搭載したエンタテインメント業界向け製品詳細情報　購入ページ
	Vectorworks Design Suite 専門分野別（建築設計/ディスプレイデザイン、ランドスケープデザイン、ステージデザイン&スポットライトプランニング）の設計支援機能、拡張機能、さらには豊富なデータライブラリを搭載した最上位の製品詳細情報　購入ページ

日	月	火	水	木	金	土
« 12月				2月 »
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

46-1. 3D基準点

VectorScript:

Python:

VectorScript:

Python:

46-2. 3D多角形

VectorScript:

Python:

VectorScript:

Python:

VectorScript:

Python:

VectorScript:

Python:

46-3. 柱状体

VectorScript:

Python:

VectorScript:

Python:

46-4. 多段柱状体

VectorScript:

Python:

VectorScript:

Python:

46-5. 3Dパス図形

VectorScript:

Python:

VectorScript:

Python:

46-6. 錐状体（汎用ソリッド）

VectorScript:

Python:

VectorScript:

Python:

46-7. 回転体

VectorScript:

Python:

VectorScript:

Python:

関連記事

この機能を利用できる製品

Vectorworks Fundamentals

Vectorworks Architect

Vectorworks Landmark

Vectorworks Spotlight

Vectorworks Design Suite