前回に引き続きアルゴリズミックデザインにご活用いただけるノードをご用意しました。「Sierpinski」ノードはフラクタル図形の一種であるシェルピンスキーのギャスケットを作成します。

コンピュータの得意な処理に「再帰」があります。ある処理を実行したとき、その処理の中で同じ処理を呼び出すことを言います。処理の結果を引き継ぎながら同じ処理を繰り返すことができます。再帰は最初はなかなか理解が難しい概念ですが、効率的向上や面白いデザインの創造に一役買ってくれる処理方法です。

この再帰処理を活用して描くことのできる図形にフラクタル図形があります。フラクタル図形は同じ形状の繰り返しで構成された図形で、どこを拡大縮小してもまた同じ図形が現れる特徴があります。

代表的なフラクタル図形には次のようなものがあります。

• • コッホ曲線
  • マンデルブロ集合
  • シェルピンスキーのギャスケット
  • ブラマンジェ曲線

フラクタル図形は自然界でも見ることができます。

• • 海岸線
  • 血管の分岐構造
  • ロマネスコのブロッコリー

フラクタルが自然界に出現する理由として、一定の体積内に理論上無限の表面積を含めることができる特性が非常に合理的であること、複雑な形状に対して、その形状を構成するために必要なルールの情報が少ないことなどが考えられています。

A&Aノードライブラリ2022 ダウンロード

24-1. シェルピンスキーのギャスケット

シェルピンスキーのギャスケットはフラクタル図形の一種で、三角形を半分の大きさの三角形で繰り返し切り欠いた図形です。このシェルピンスキーのギャスケットが木漏れ日に近い効果を得られるとして、日除けを設計する研究もされるなど建築の分野でも活用されています。

シェルピンスキーのギャスケットは次の手順で作成されます。

1. 1. 正三角形を用意する
   2. 正三角形の各辺の中点を互いに結んで半分の大きさかつ逆さの正三角形を作成する。
   3. 元の正三角形を逆さの正三角形で切りかく。
   4. 残った正三角形に対して2、3の手順を何度も繰り返す。

• • 2回繰り返したシェルピンスキーのギャスケット

• • 10回繰り返したシェルピンスキーのギャスケット

24-2. Sierpinski ノード

A&Aノードライブラリに新しいノードを追加しました。フラクタル図形の作図にご利用いただける3種のノードです。

• • Sierpinski
  • Sierpinski 3D
  • Tetra Mesh

Sierpinskiノードは指定した三角形内にシェルピンスキーのギャスケットを生成してギャスケット内の全て三角形を出力します。

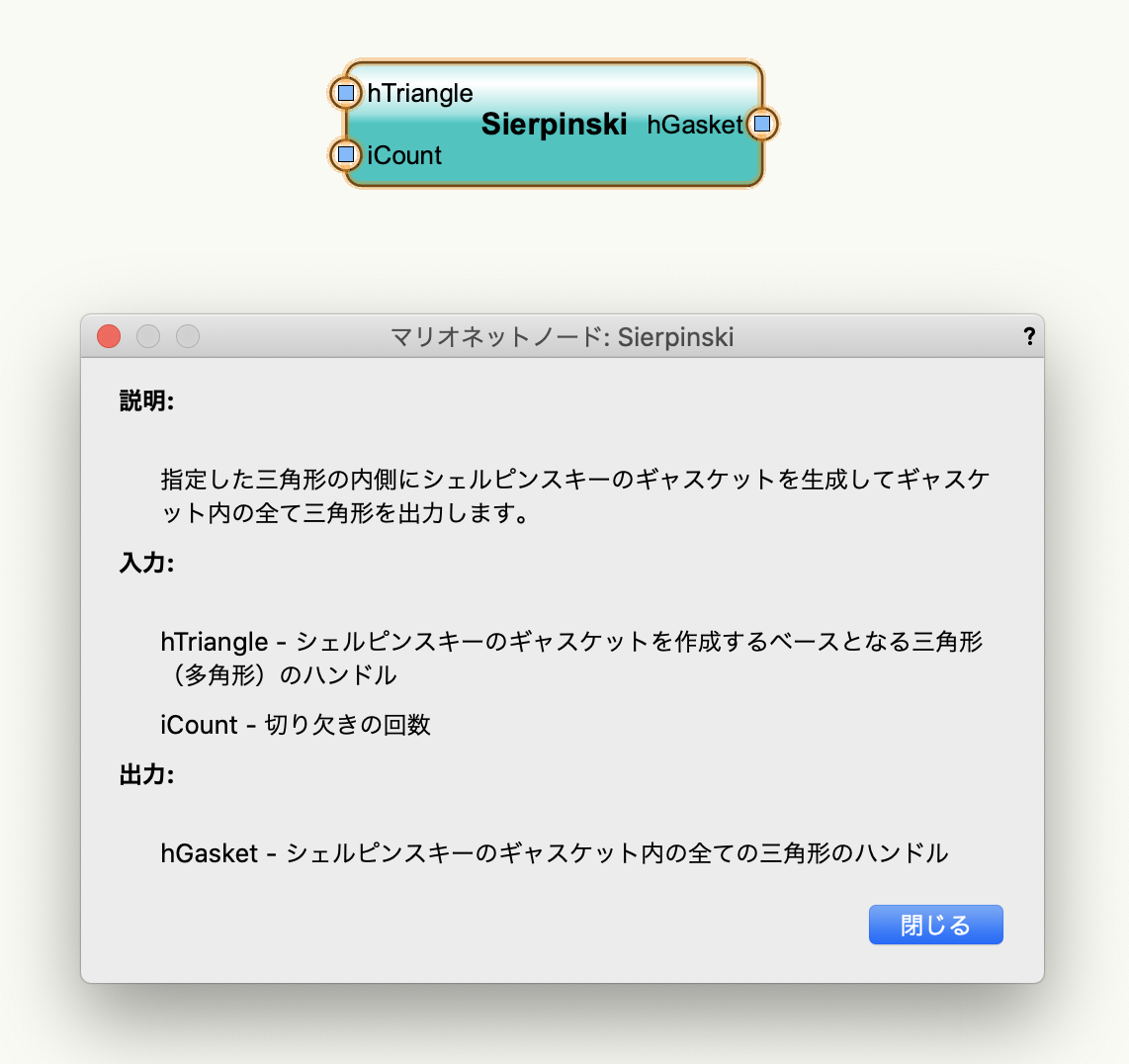
入力

• • hTriangle：シェルピンスキーのギャスケットを作成するベースとなる三角形（多角形）のハンドルを入力します。
  • iCount：切り欠きの回数を整数で指定します。

出力

24-2-1. ノードの使い方

Sierpinskiノードを使用してシェルピンスキーのギャスケットを作成します。

まずはRegular Polygonノードを使用して正三角形を作成します。Regular Polygonノードは辺の数を指定して簡単に正三角形を作成できる便利なノードです。「図形 > 2D」カテゴリから見つけてください。

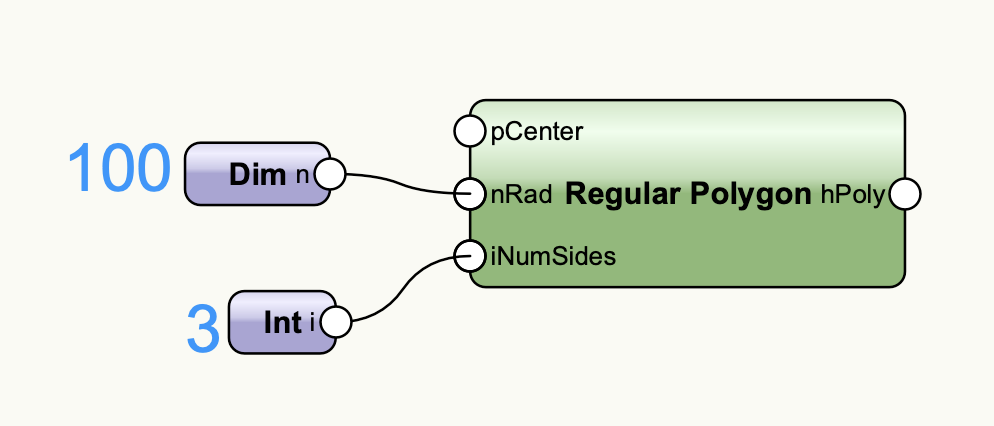
正三角形が生成されました。

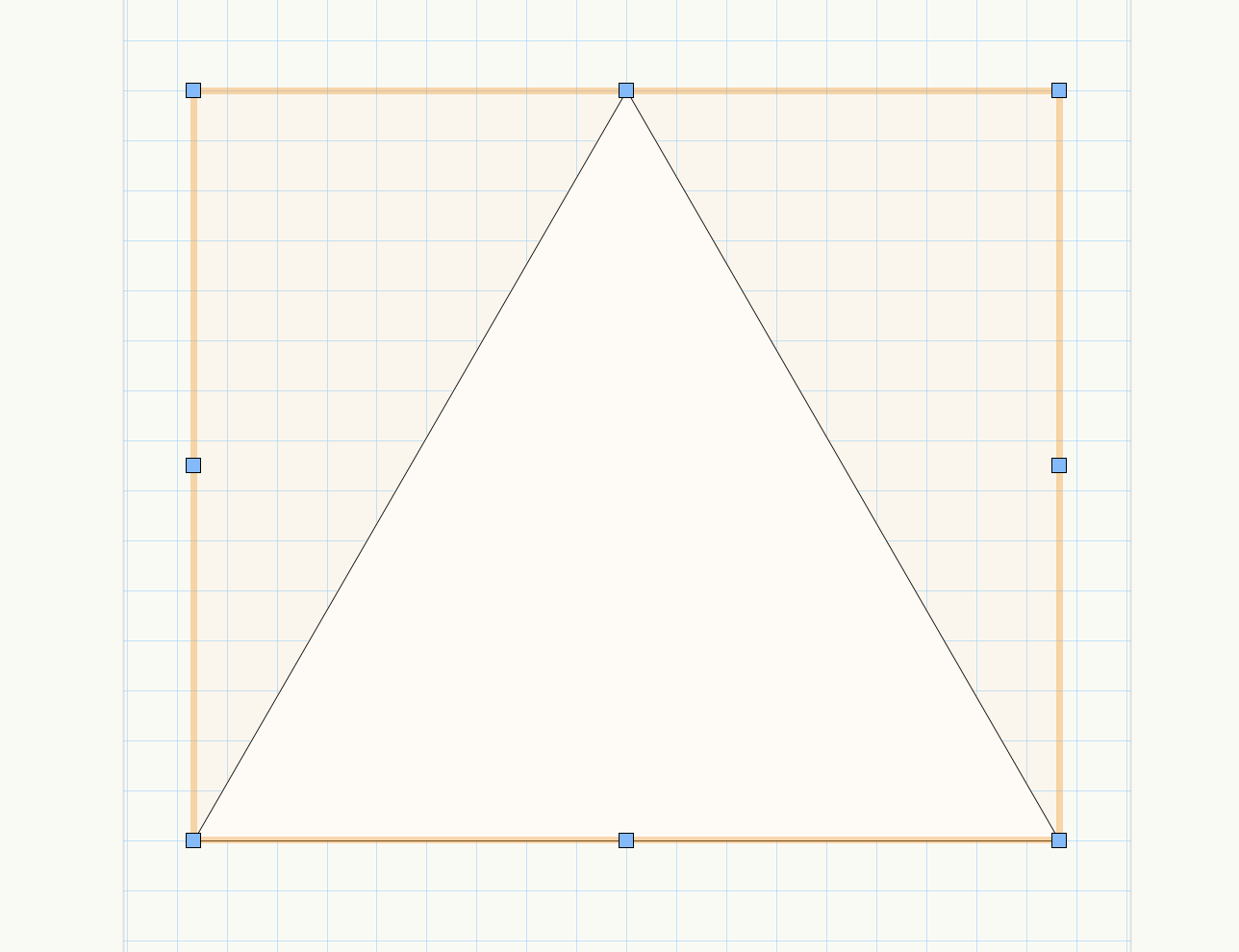
この三角形をSierpinskiノードにベースの三角形として入力します。ここでは切り欠き回数を1回とします。

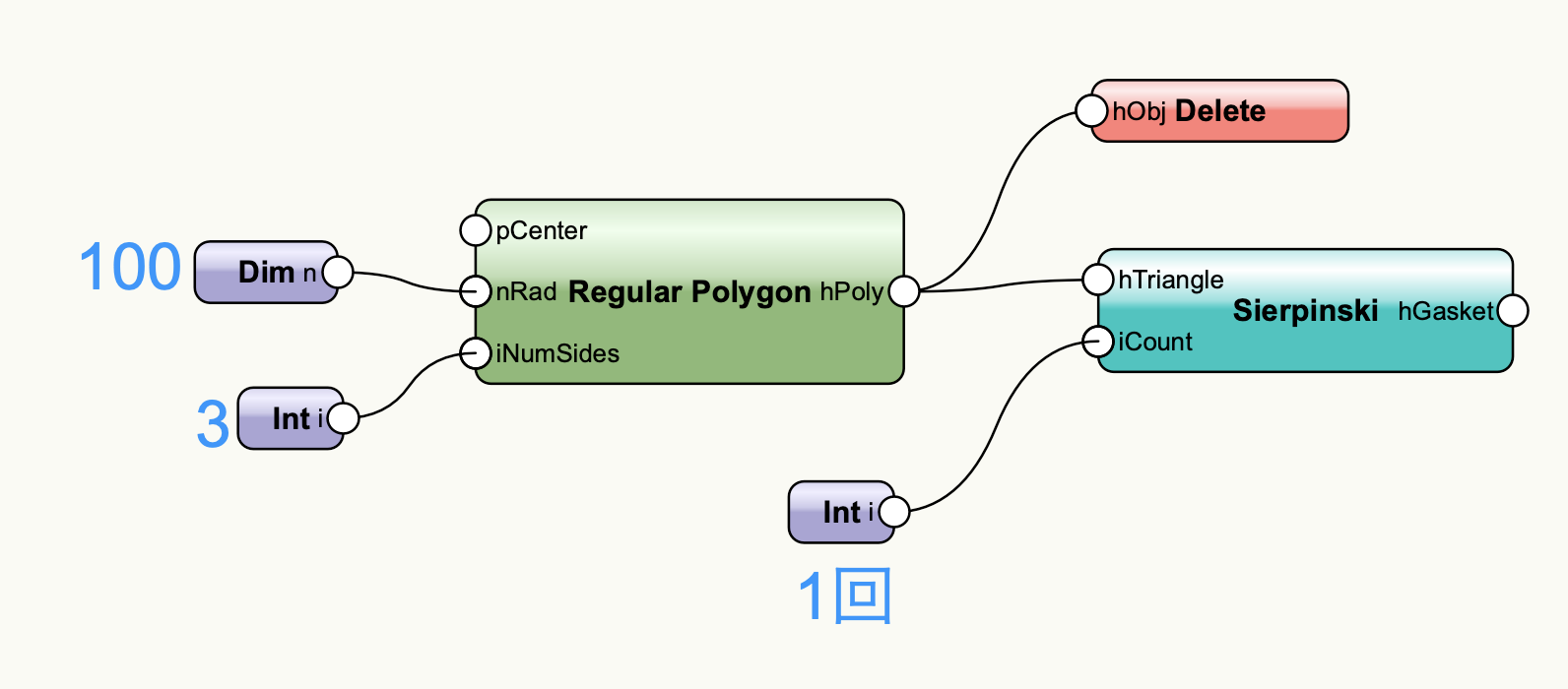
実行します。切り欠きが1回実行されて3つの三角形が生成されました。

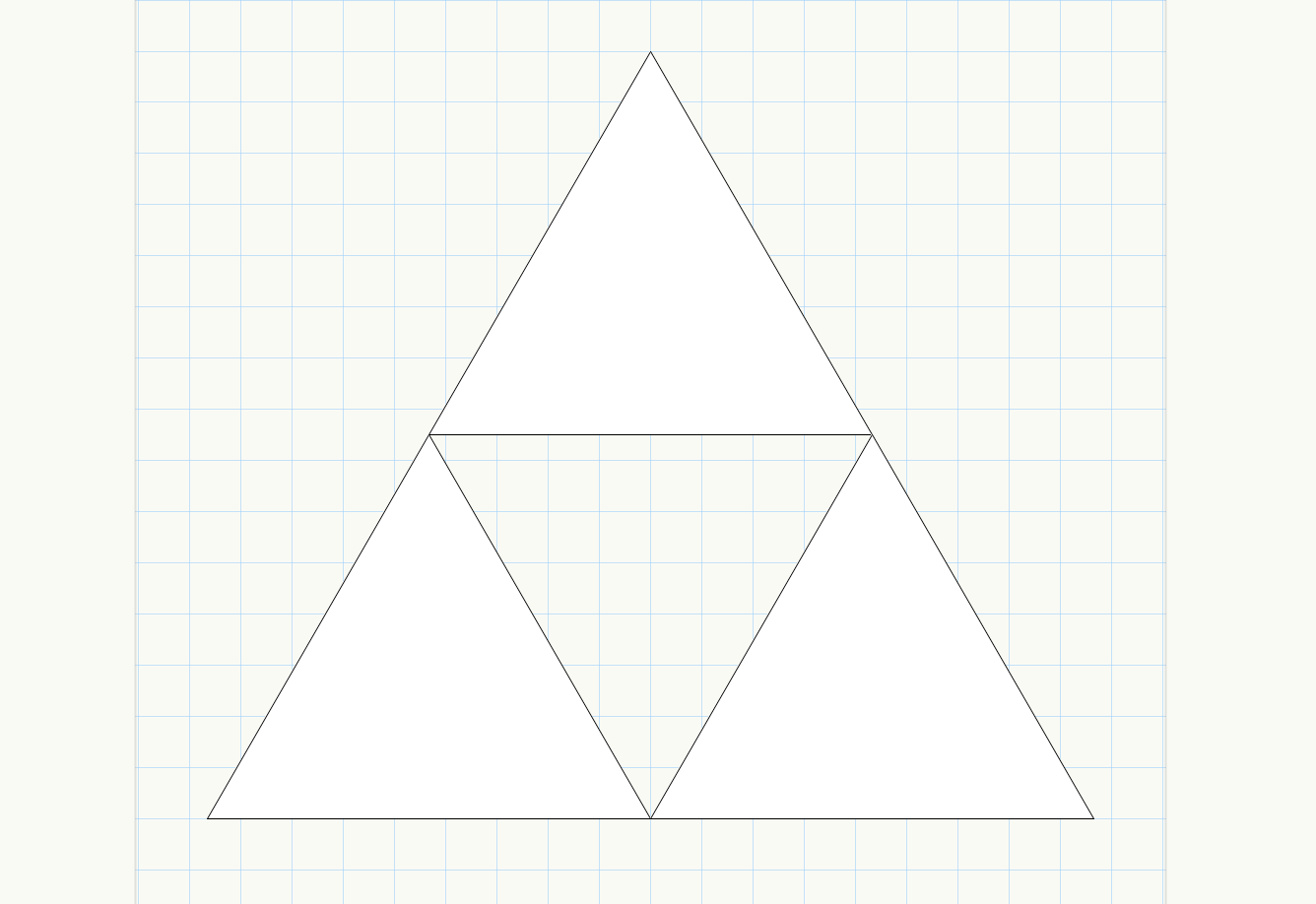
切り欠き回数を2回に変更して再度実行します。3×3で9つの三角形になります。

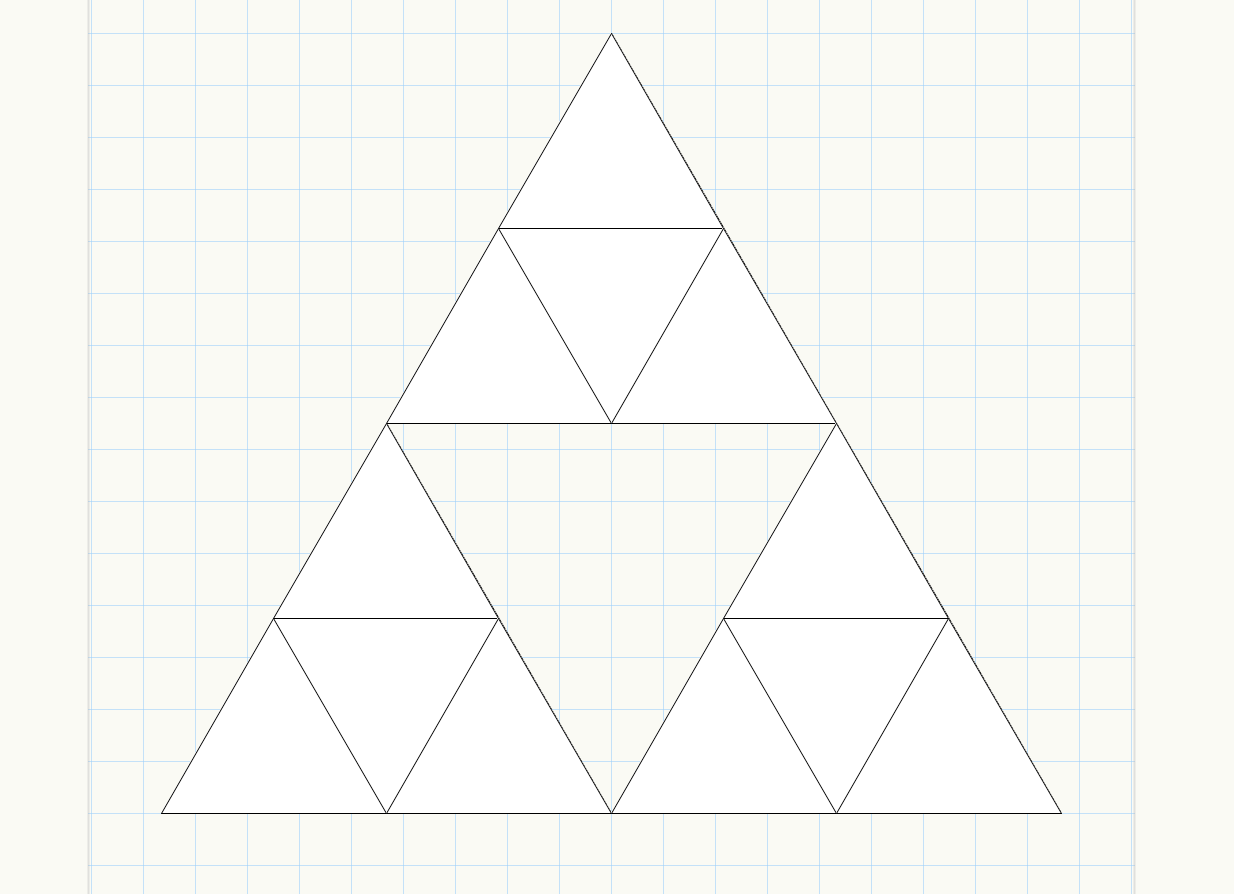
このように切り欠きの回数をnとすると、3のn乗個の三角形が生成されます。

Sierpinskiノードは連続して使用することもできます。例えば、切り欠き回数1回のSierpinskiノードの3つ繋げると、3回切り欠いたときと同じ結果が得られます。

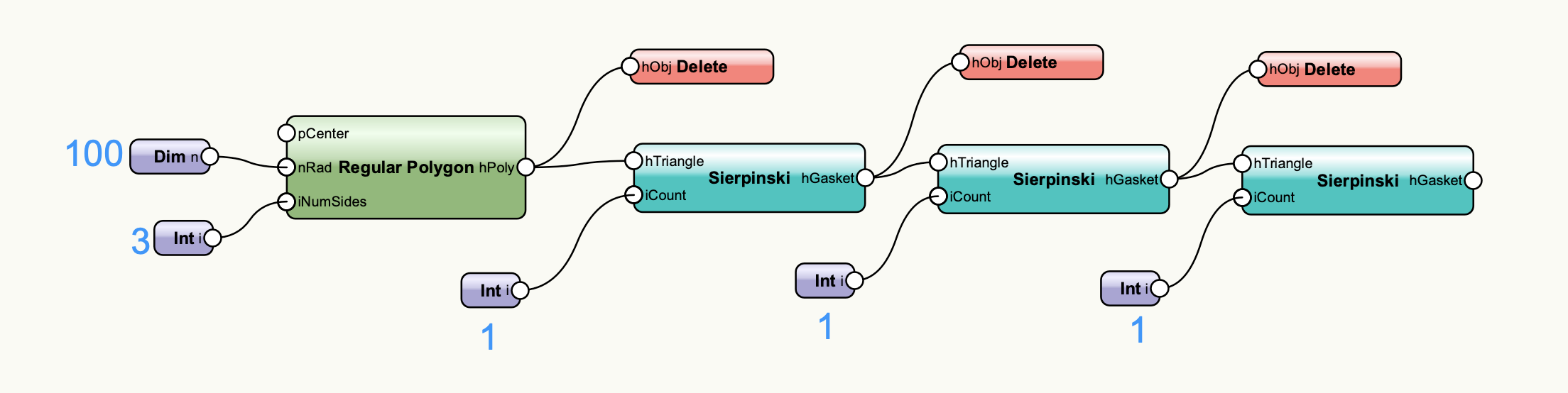
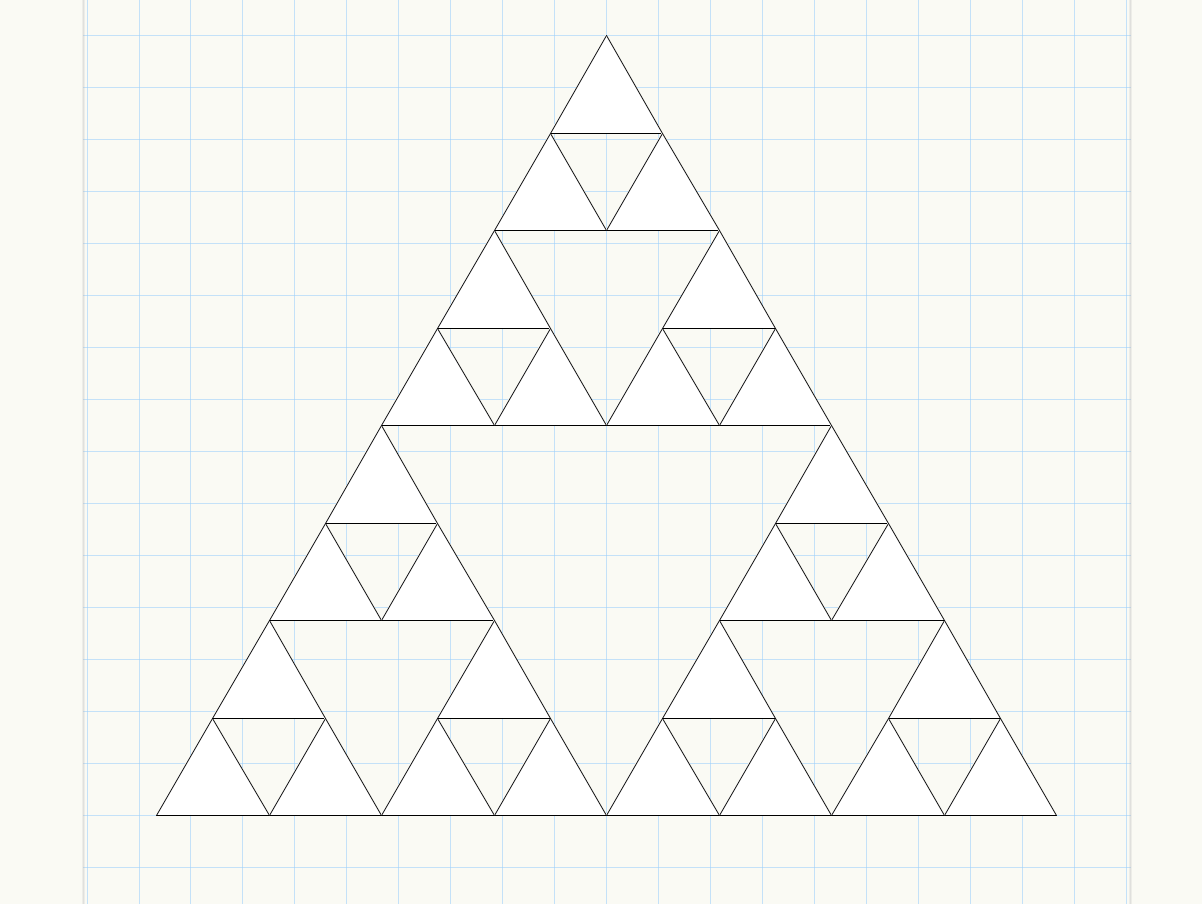
同じノードが連続して配置されたネットワークは再帰らしい見た目で好みです。途中のワイヤーにAttributeノードを挟めば、生成過程の可視化などに活用できそうですね。

24-3. Sierpinski 3D ノード

Sierpinski 3Dノードはシェルピンスキー四面体を作成します。シェルピンスキー四面体はシェルピンスキーのギャスケットを3次元化したようなイメージで、ギャスケットと同様の操作で四面体の各辺の中点で作成できる四面体で削り取りを繰り返し行った図形です。

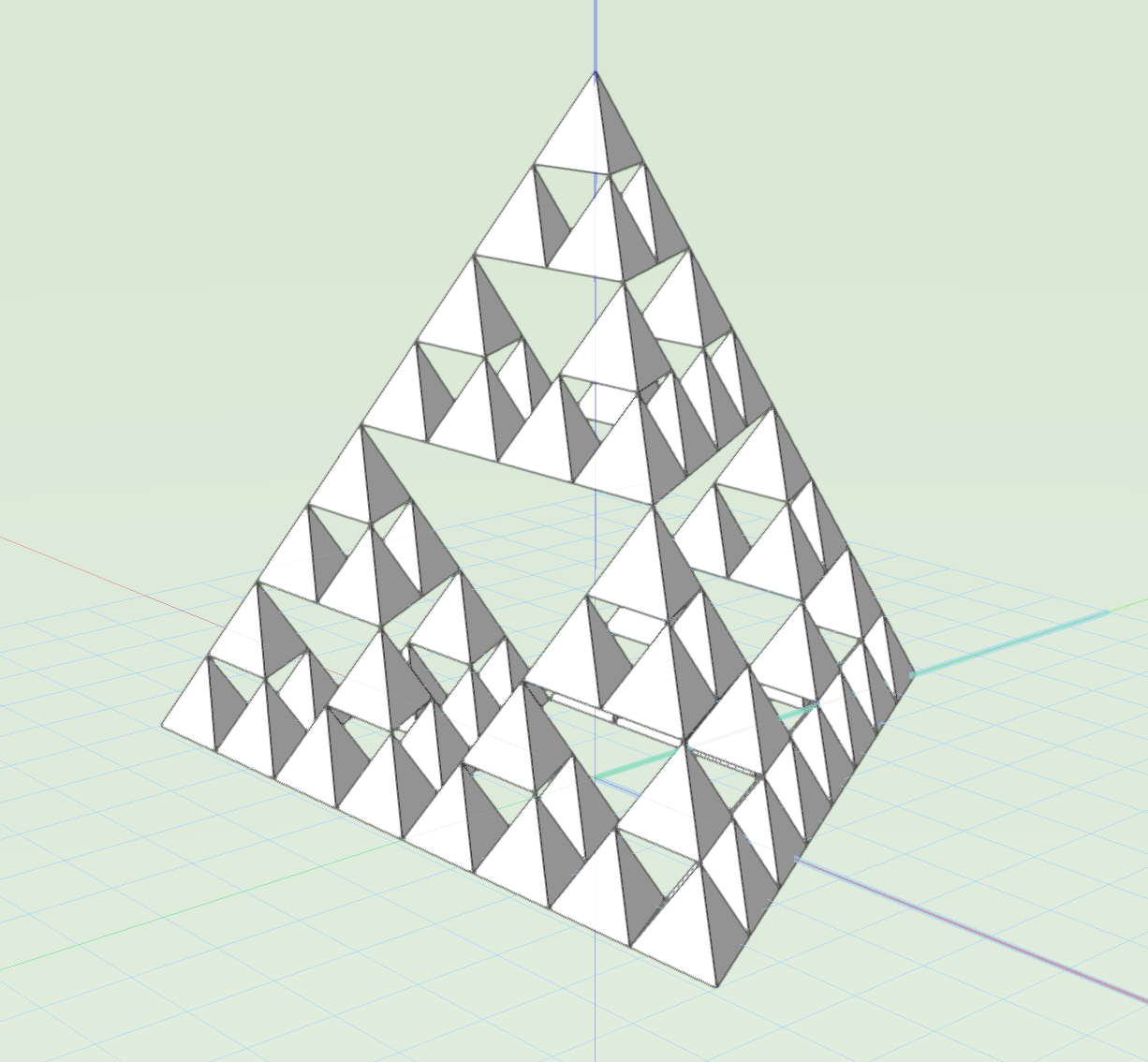
Sierpinski 3Dノードは指定した四面体内にシェルピンスキー四面体を生成して四面体内の全て四面体の4点の座標のリストを出力します。

入力

• • hTetra：ベースの四面体のメッシュ図形のハンドルを入力します。
  • iCount：削り取りの回数を整数で指定します。

出力

• • pTetrahedron：生成したシェルピンスキーのギャスケット内の全ての三角形の座標のリストを出力します。

24-3-1. Tetra Mesh ノード

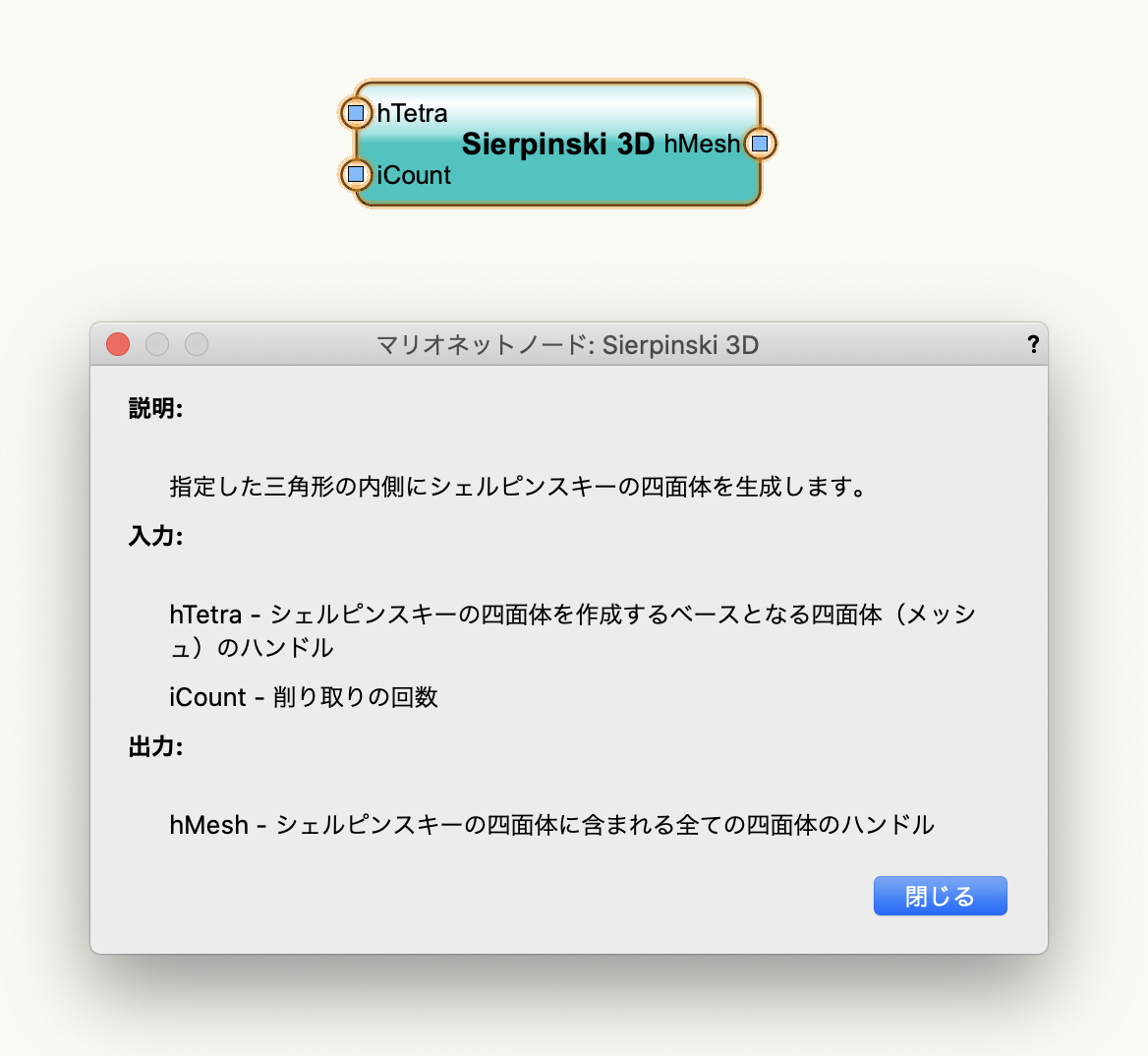
Tetra Meshノードは正四面体のメッシュ図形を作成します。Sierpinski 3Dノードで必要となるベースの四面体を作成するのに使用します。

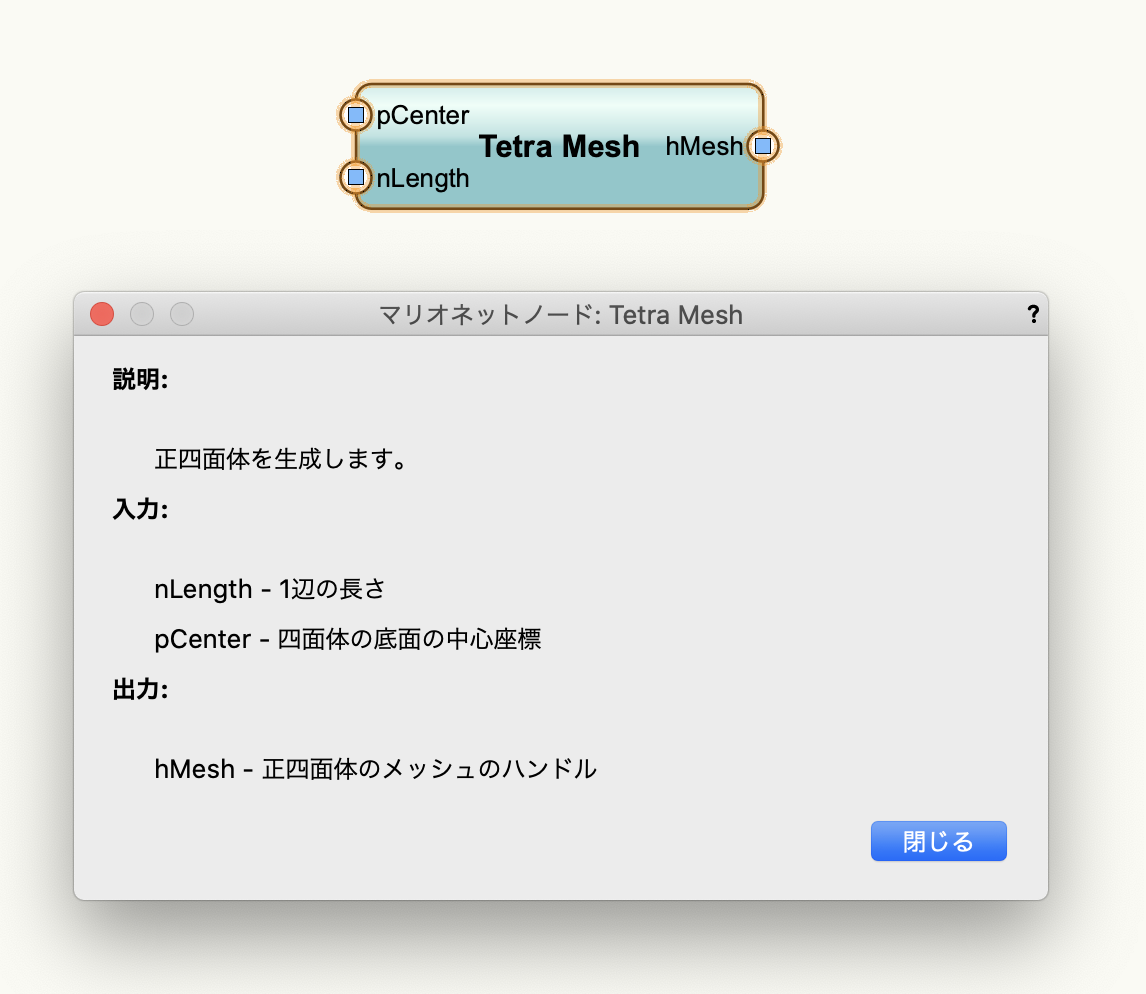
入力

• • pCenter：底面の中心座標を指定します。
  • nLength：1辺の長さの寸法値を入力します。

出力

• • hMesh：生成した四面体のメッシュ図形のハンドルを出力します。

24-3-2. ノードの使い方

Sierpinski 3Dノードを使用してシェルピンスキーの四面体を作成します。

まずはTetra Meshノードを使用して四面体を作成します。ここでは1辺の長さは100mmとします。

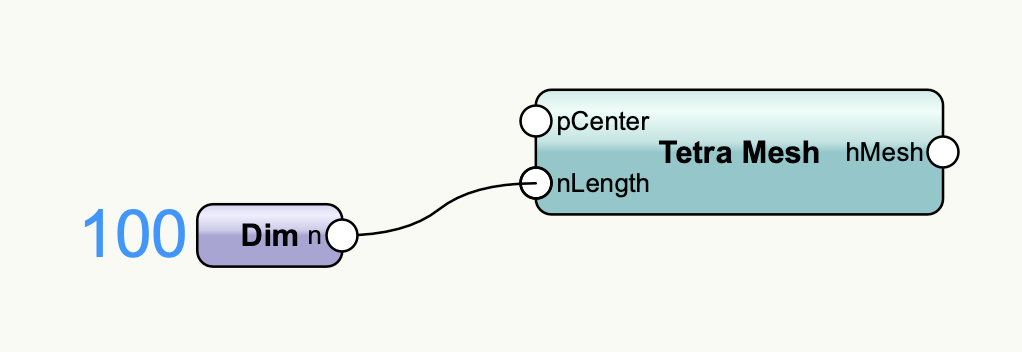
1辺を100mmとした正四面体のメッシュが作成されます。

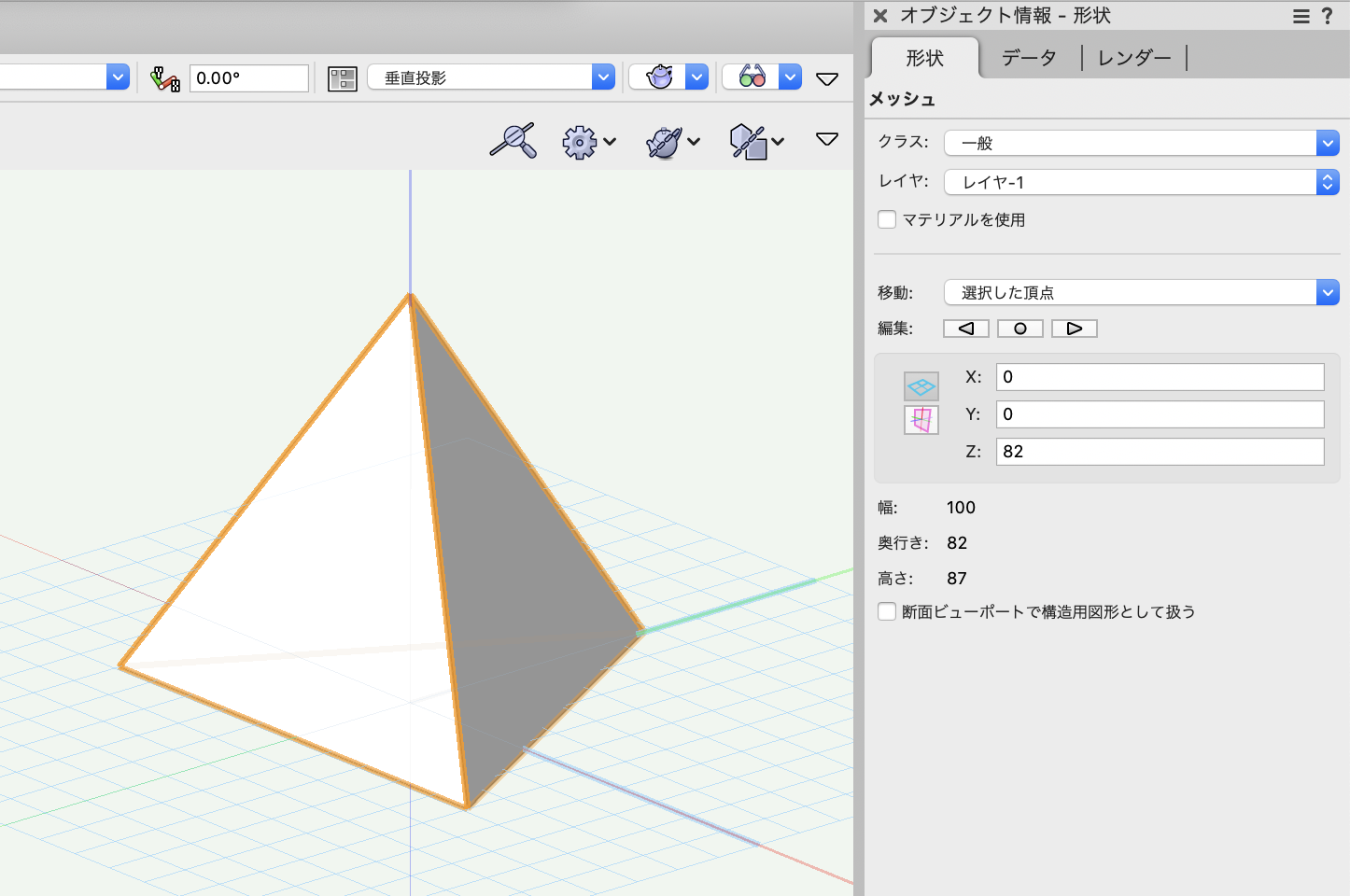
中に入ると、4面の3D多角形図形で構成されているのが分かります。

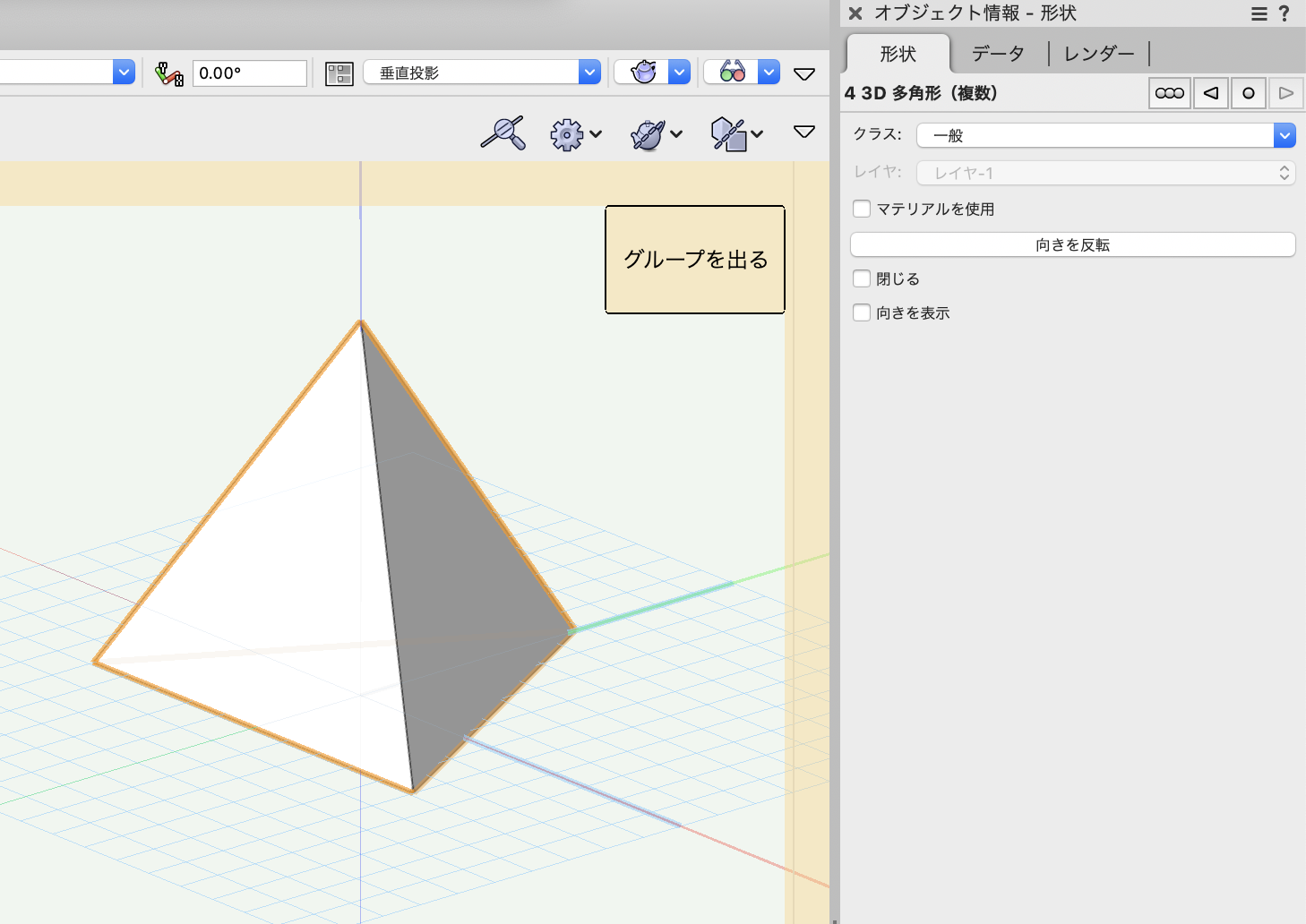
この四面体をSierpinski 3Dノードにベースの四面体として入力します。

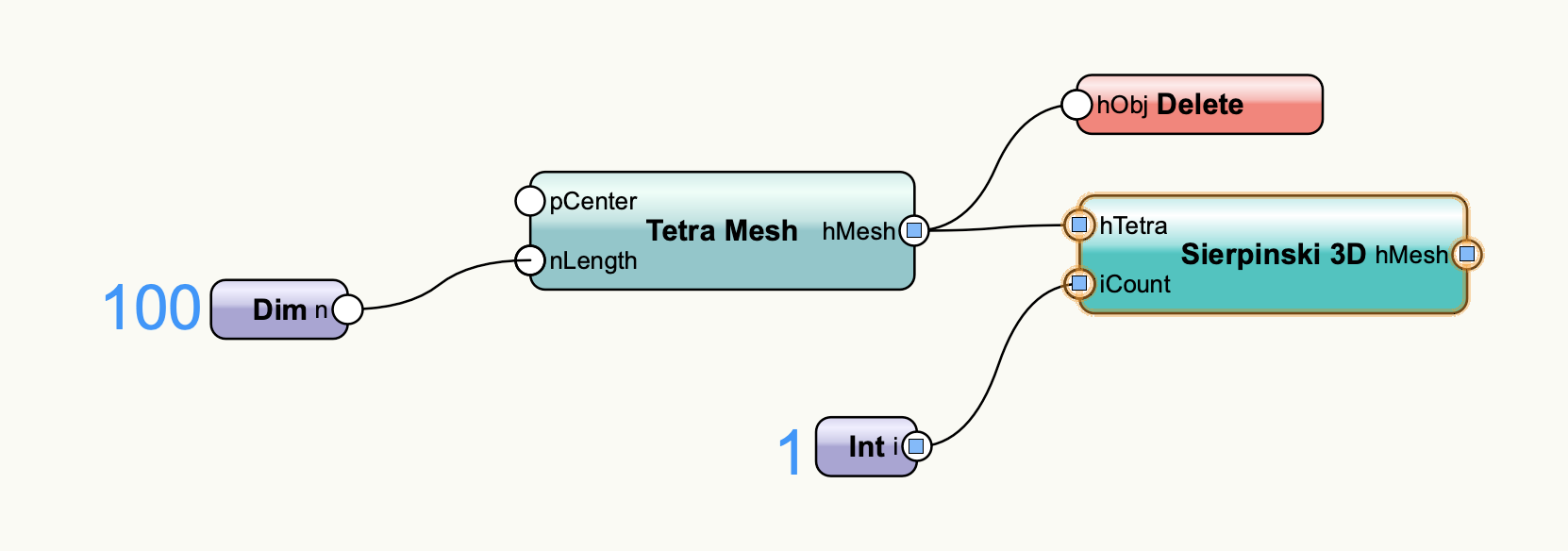
プログラムを実行します。削り取りが1度実行されて4つの四面体が生成されました。

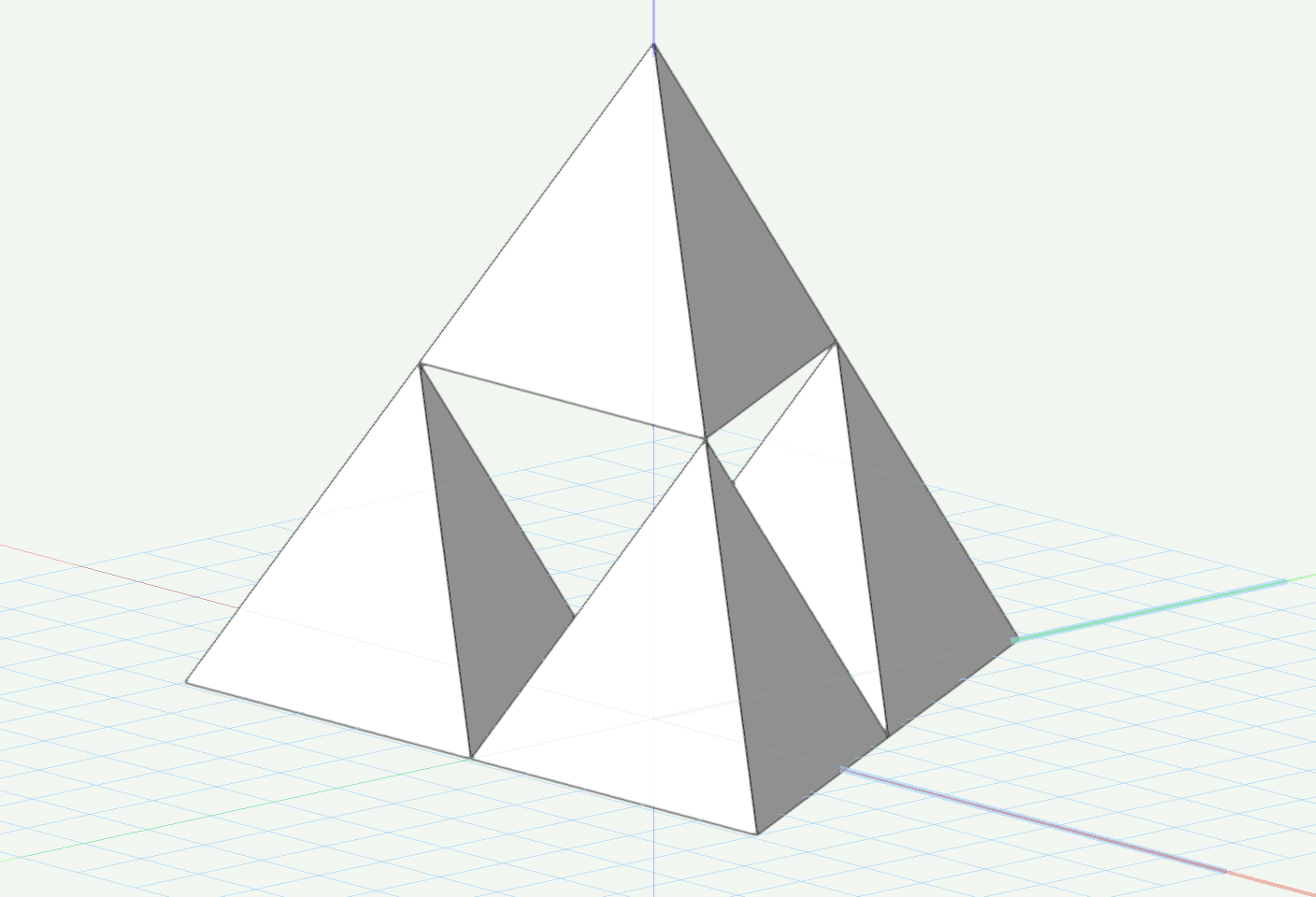
使い方はSierpinskiノードと同様です。削り取りの回数を増やすと指数関数的に穴が増えていきます。削り取り回数がn回のとき、4のn乗個の四面体が生成されます。

24-4. 影をつくる

日除けの研究を読んで実際どんな影ができるのか気になリましたので、簡単にシミュレーションしてみます。

配列状に並べた四面体をそれぞれSierpinski 3Dノードを適用して太陽光を透過させる方法で影をつくります。

まずはSeriesとMix2の組み合わせで5×5の配列状の座標を作成します。

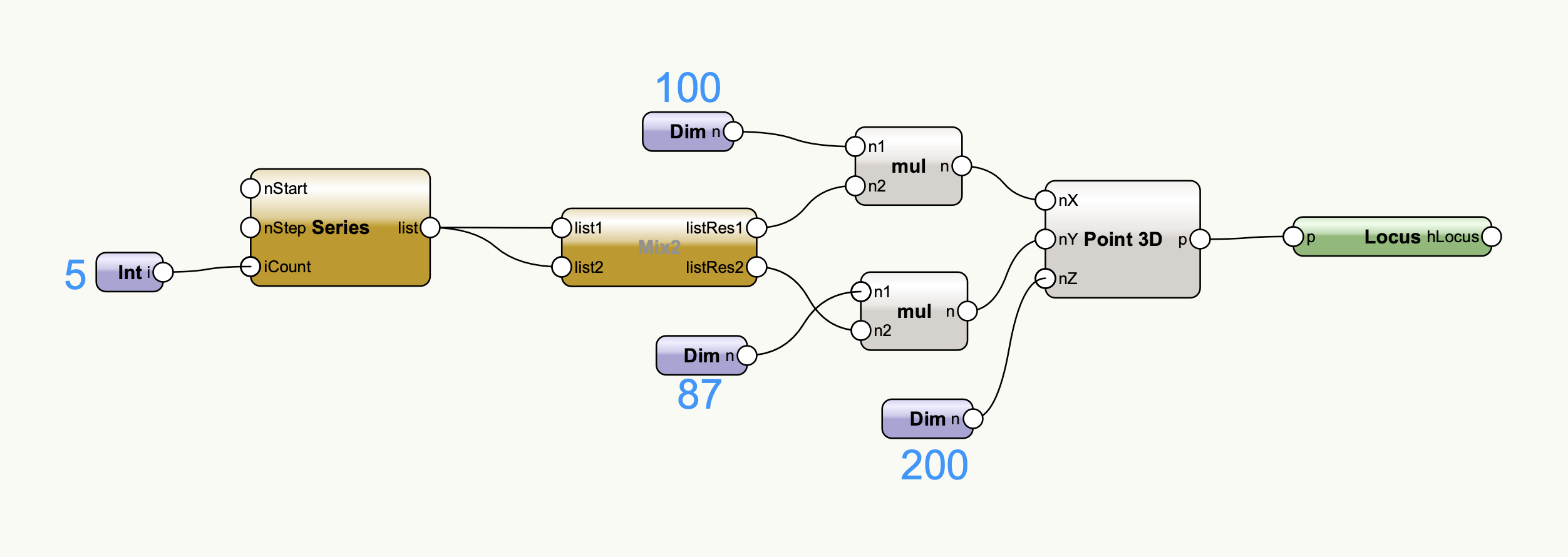
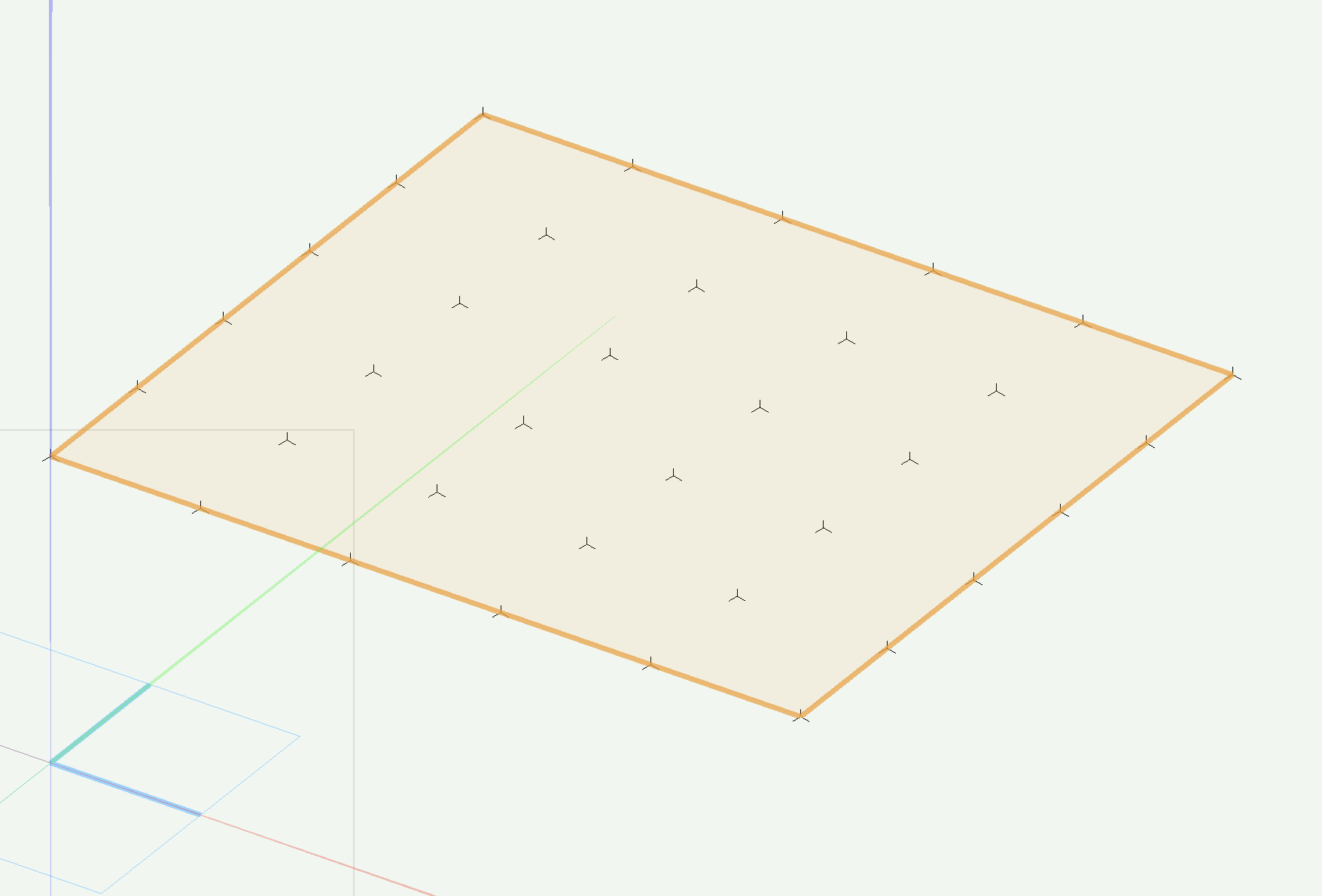
Tetra Meshノードで作成した四面体をこの配列に並べます。

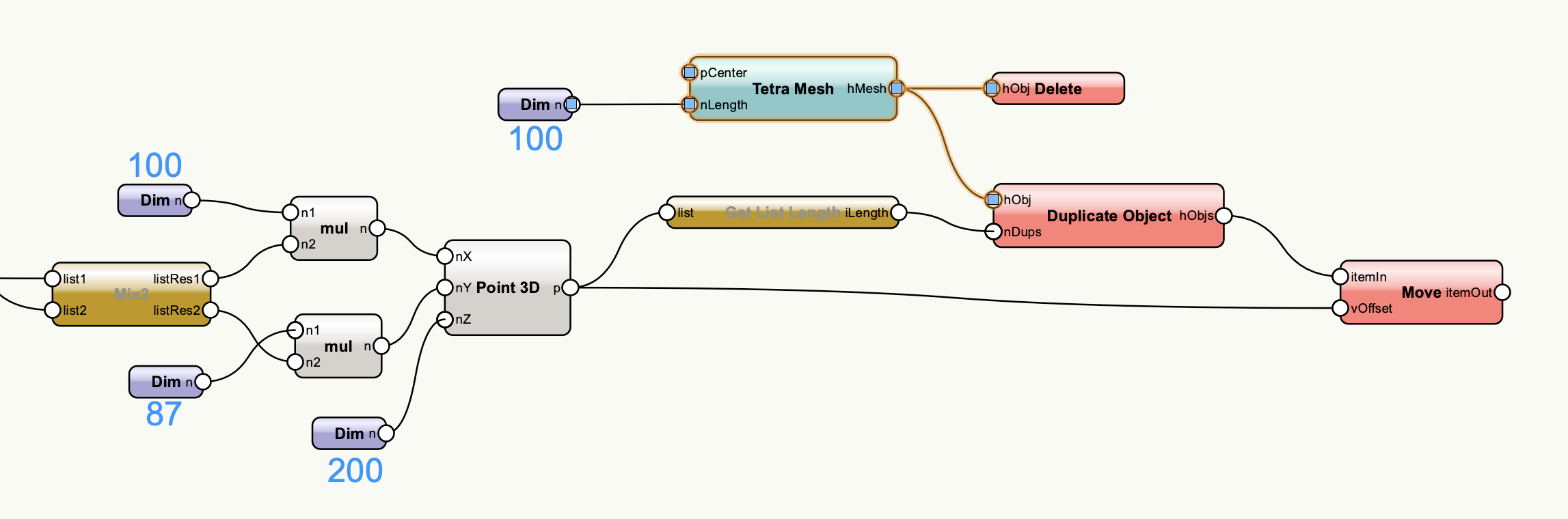
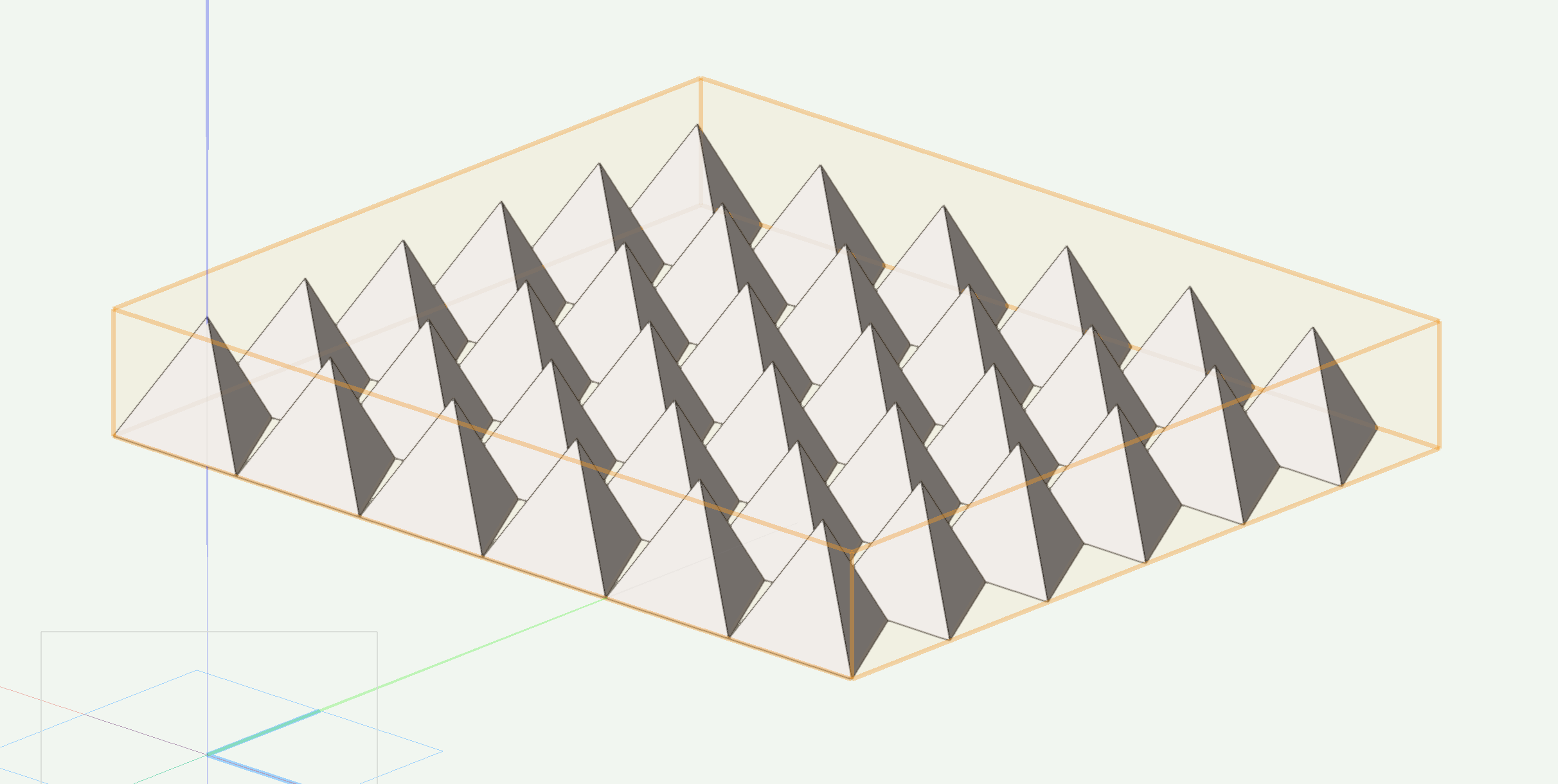
Sierpinski 3Dノードでシェルピンスキーの四面体に変換します。削り取り回数は3回とします。

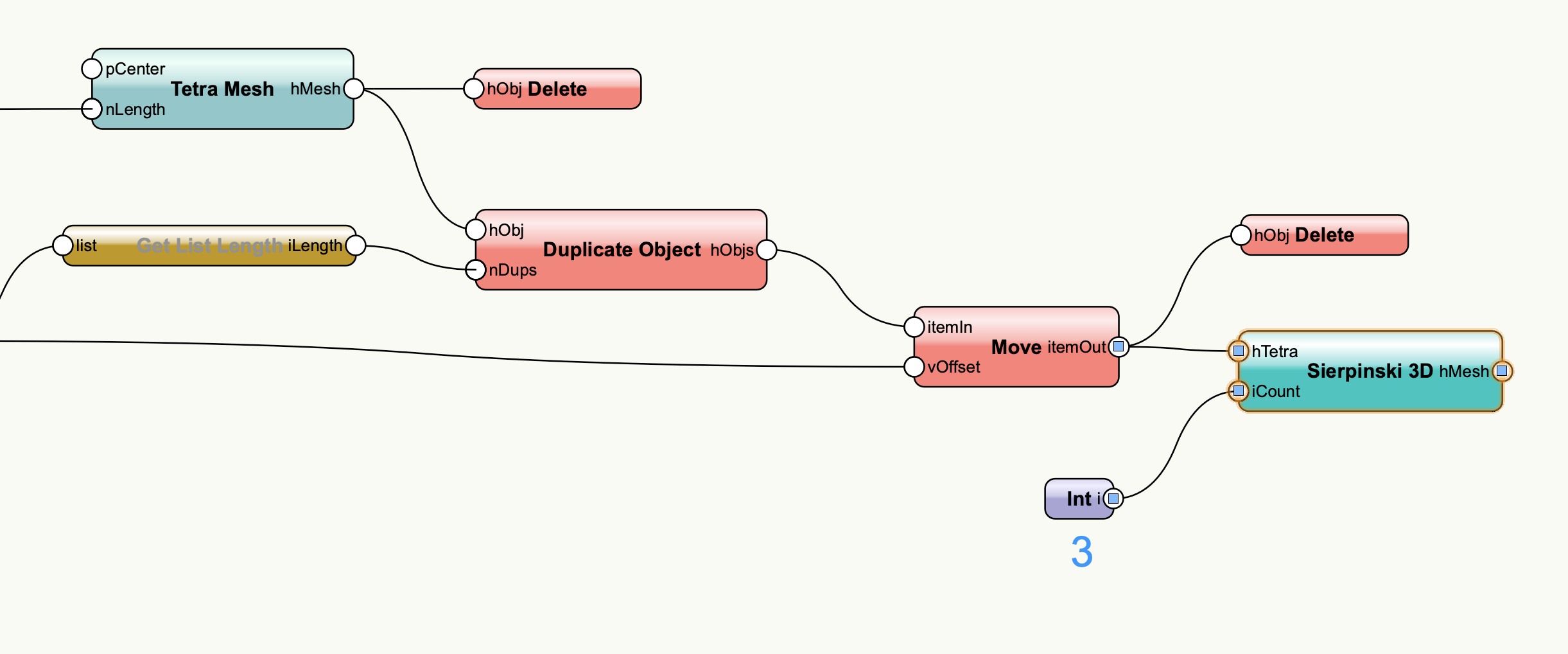
屋根状のシェルピンスキー四面体ができました。

影を落とす地面を簡単に柱状体で作成します。さらに、太陽光設定オブジェクトを配置して、夏の暑い日の一番暑い時間に設定します。

レンダリングを実行します。影が落ちました。

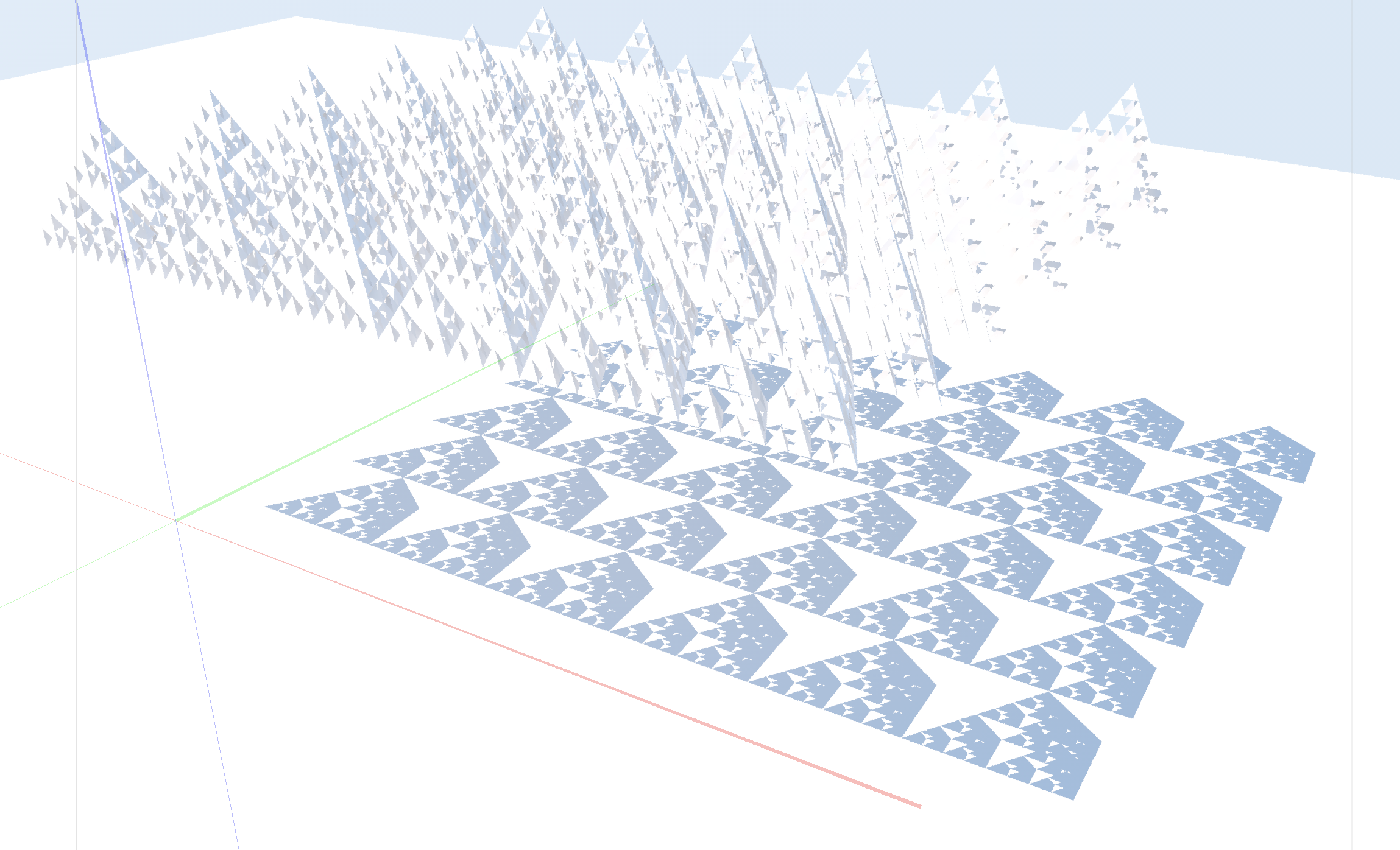
木漏れ日のような鱗のような面白いかたちですね。配置パターンを変えたり、削り取りの回数を変えてもまた違った影が作ることができそうです。

再帰やフラクタルについては解説を読むよりも数字や図形で実際に触れてみることが理解への近道です。まずは今回ご紹介したノードを使用してフラクタルの造る不思議な空間を体験してください。

A&Aノードライブラリ2022 ダウンロード